题目内容
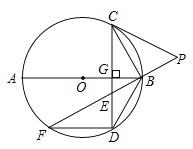
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 交
交![]() 于
于![]() ,
,![]() 的外接圆
的外接圆![]() 与边
与边![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)在(2)的条件下,求![]() 的长.
的长.
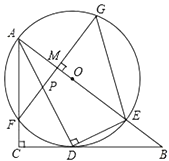
【答案】(1)见解析;(2)6;(3)![]()
【解析】
(1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
(1)证明:连结![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的直径,即
的直径,即![]() 在
在![]() 上,
上,
∵![]() 是角平分线,
是角平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() 是
是![]() 的切线;
的切线;
(2)解:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
解得,![]() ,
,![]() (舍),(注:也可由
(舍),(注:也可由![]() 得
得![]() ),
),
∴![]() ,即
,即![]() 的半径为6;
的半径为6;
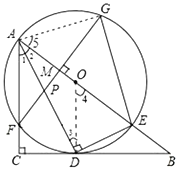
(3)解:连结![]() ,则
,则![]() ,
,![]() .
.
∴![]() ,
,
即![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
即![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目