题目内容
【题目】问题提出:

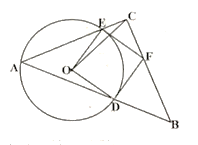
(1)如图①,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是 .
问题探究:
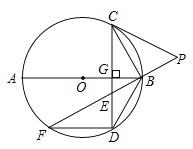
(2)如图②,在边长为10的正方形ABCD中,点G是BC边的中点,E、F分别是AD和CD边上的点,请探究并求出四边形BEFG的周长的最小值.
问题解决:
(3)如图③,四边形ABCD中,AB=AD=6,∠BAD=60°,∠BCD=120°,四边形ABCD的周长是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
【答案】(1)25;(2)四边形BEFG的周长的最小值为30;(3)四边形ABCD的周长最大值为12+4![]() .
.
【解析】
(1)如图1,点P运动至半圆O的中点时,底边AB上的高最大,即P'O=r=5,求出此时△P'AB的面积即可;
(2)如图2,作点G关于CD的对称点G′,作点B关于AD的对称点B′,连接B′G′,B′E,FG′,根据两点之间线段最短即可解决问题;
(3)如图3,连接AC、BD,在AC上取一点,使得DM=DC,首先证明AC=CD+CB,再证明当AC为△ABC的外接圆的直径时,四边形ABCD的周长最大.
(1)如图1,点P运动至半圆O的中点时,底边AB上的高最大,即P'O=r=5,
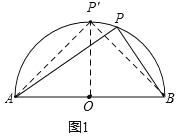
此时△PAB的面积最大值,
∴S△P'AB![]() 10×5=25,
10×5=25,
故答案为:25;
(2)如图2,作点G关于CD的对称点G',作点B关于AD的对称点B',连接B'G',B'E,FG',
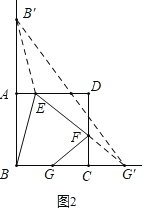
∵EB=EB',FG=FG',
∴BE+EF+FG+BG=B'E+EF+FG'+BG,
∵EB'+EF+FG'≥B'G',
∴四边形BEFG的周长的最小值=BG+B'G',
∵BG![]() BC=5,BB'=20,BG'=15,
BC=5,BB'=20,BG'=15,
∴B'G'![]() 25,
25,
∴四边形BEFG的周长的最小值为30;
(3)如图3,连接AC、BD,在AC上取一点,使得DM=DC,
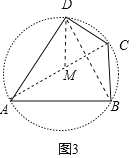
∵∠DAB=60°,∠DCB=120°,
∴∠DAB+∠DCB=180°,
∴A、B、C、D四点共圆,
∵AD=AB,∠DAB=60°,
∴△ADB是等边三角形,
∴∠ABD=∠ADB=60°,
∴∠ACD=∠ADB=60°,
∵DM=DC,
∴△DMC是等边三角形,
∴∠ADB=∠MDC=60°,CM=DC,
∴∠ADM=∠BDC,
∵AD=BD,
∴△ADM≌△BDC(SAS),
∴AM=BC,
∴AC=AM+MC=BC+CD,
∵四边形ABCD的周长=AD+AB+CD+BC=AD+AB+AC,
∵AD=AB=6,
∴当AC最大时,四边形ABCD的周长最大,
∴当AC为△ABC的外接圆的直径时,四边形ABCD的周长最大,
∵![]() ,
,
∴AC的最大值=4![]() ,
,
∴四边形ABCD的周长最大值为12+4![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】国家教育部提出“每天锻炼一小时,健康工作五十年,幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么?”,规定从“打球”,“跑步”,“游泳”,“跳绳”,“其他”五个选项中选择自己最喜欢的项目,且只能选择一个项目,并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
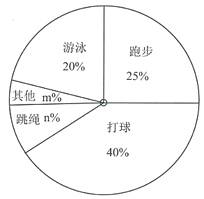
(1)这次问卷调查的学生总人数为 ,人数![]() ;
;
(2)扇形统计图中,![]() ,“其他”对应的扇形的圆心角的度数为 度;
,“其他”对应的扇形的圆心角的度数为 度;
(3)若该年级有1200名学生,估计喜欢“跳绳”项目的学生大约有多少人?