Question

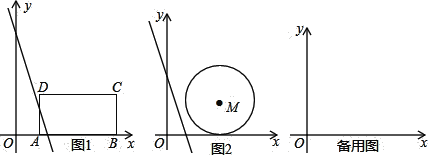
【题目】如图1，在平面直角坐标系中，有一矩形ABCD，其三个顶点的坐标分别为A(2，0)，B(8，0)，C(8，3)，将直线l：以每秒3个单位的速度向右运动，设运动时间为t秒．

（1）当t＝ 时，直线l经过点A（直接填写答案）；

（2）设直线l扫过矩形ABCD的面积为S，试求S＞0时S与t的函数关系式；

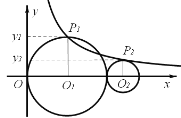
（3）在第一象限有一半径为3、且与两坐标轴恰好都相切的⊙M，在直线l出发的同时，⊙M以每秒2个单位的速度向右运动，如图2，则当t为何值时，直线l与⊙M相切？

Answer 1

【答案】（1）1;

（2）当1＜t≤时,S＝;

当＜t≤3时,S＝9t－;

当3＜t≤时,S＝－(3t－10)2＋18;

当t＞时,S＝18;

（3）t＝5－或t＝5＋．

【解析】

试题分析:（1）y＝－3x－3与x轴交点坐标是（-1,0）,直线l经过点A（2,0）,故向右平移3个单位长度,直线l:y＝－3x－3以每秒3个单位的速度向右运动,所以t=1;

（2）求出直线l:y=﹣3x+9t﹣3,再分情况讨论;

（3）分两种情况讨论,借助三角形相似即可．

试题解析:(1)y＝－3x－3与x轴交点坐标是（-1,0）,直线l经过点A（2,0）,故向右平移3个单位长度,直线l:y＝－3x－3以每秒3个单位的速度向右运动,所以t=1;

（2）由题意,可知矩形ABCD顶点D的坐标为(2,3)．

由一次函数的性质可知,当t由小到大变化时,直线l:y=﹣3(x﹣3t)-3=﹣3x+9t﹣3向右平移,依次扫过矩形ABCD的不同部分．

可得当直线经过A(2,0)时,t=1;当直线经过D(2,3)时,t=;当直线经过B(8,0)时,t=3;当直线经过C(8,3)时,t=．

①当1＜t≤时, 如图所示．

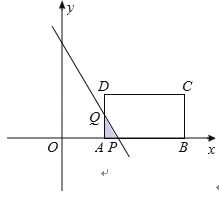
设直线l:y=-3x+9t﹣3与x轴交于点P,与AD交于点Q．

令y=0,可得x=3t﹣1,∴AP=3t﹣3;

令x=2,可得y=9t﹣9,∴AQ=9t﹣9．

∴S=S△APQ=APAQ=(3t﹣3)( 9t﹣9)=;

<>②当＜t≤3时,如图所示．

设直线l:y=-3x+9t﹣3与x轴交于点P,与CD交于点Q．

令y=0,可得x=3t﹣1,∴AP=3t﹣3;

令y=3,可得x=3t﹣2,∴DQ=3t﹣4．

S=S梯形APQD=(DQ+AP)AD=9t－;

③当3＜t≤时,如图所示．

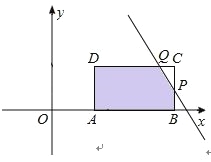
设直线l:y=-3x+9t﹣3与BC交于点P,与CD交于点Q．

令x=8,可得y=9t﹣27,∴BP=9t﹣27,CP=30﹣9t;

令y=3,可得x= 3t﹣2,∴DQ= 3t﹣4,CQ=10﹣3t．

S=S矩形ABCD﹣S△PQC=18﹣CPCQ=－(3t－10)2＋18;

④当t＞时,S=S矩形ABCD=18．

综上所述, S与t的函数关系式为:

;

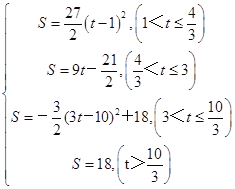(3)若直线l:y=﹣3x+9t﹣3与⊙M相切,如图所示,应有两条符合条件的切线．

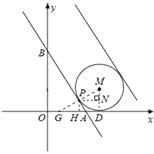
设直线与x轴、y轴交于A、B点,则A(3t﹣1,0)、B(0,9t﹣3),∴OB=3OA．

由题意,可知⊙M与x轴相切,设切点为D,连接MD;

设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;过P点作PN⊥MD于点N,PH⊥x轴于点H．

易证△PMN∽△BAO,∴PN:MN=OB:OA=3,∴PN=3MN．

在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得: MN=,PN=,

∴PH=ND=MD﹣MN=3﹣,OH=OD﹣HD=OD﹣PN=2t+3﹣,

∴P(2t+3﹣,3﹣),代入直线解析式求得:t=5﹣;

同理,当切线位于另外一侧时,可求得:t=5+．

考点:动点问题．