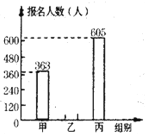
题目内容
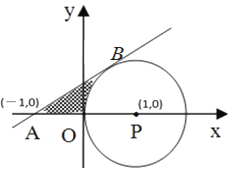
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中
三点,其中![]() ,曲线
,曲线![]() 分别与线段
分别与线段![]() ,
,![]() 交于点
交于点![]() ,
,![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)当![]() 时,求
时,求![]() 的面积;
的面积;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将t=1代入得到A、B、C的坐标以及曲线的函数解析式,进而可求得直线BC的函数解析式,再将曲线与直线的解析式联立方程组求解即可;
(2)根据A、C两点坐标表示出直线AC的解析式,与曲线解析式联立方程组可得到点E坐标,再由![]() 求得t的值,从而可求值直线BC及曲线的解析式,进而求解即可;
求得t的值,从而可求值直线BC及曲线的解析式,进而求解即可;
(3)先用直线BC与曲线联立方程组表示出点D坐标,再用直线AC与曲线联立方程组表示出点E坐标,最后根据![]() 求得t的值即可.
求得t的值即可.
解:(1)设直线![]() 解析式为
解析式为![]() ,
,
∵直线过点![]() ,
,![]() ,
,
∴直线![]() :
:![]() .
.
当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 的横坐标满足
的横坐标满足
![]() ,解得
,解得![]() 或
或![]() .
.
∵![]() 的横坐标在0到1之间,∴
的横坐标在0到1之间,∴![]() .
.
∴![]() .
.
(2)解:∵![]() ,
,![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() .
.
∴直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 的纵坐标为
的纵坐标为![]() .
.![]() .
.
∵![]() ,∴当
,∴当![]() 时,
时,![]() .(负解舍去)
.(负解舍去)
∴![]() 所在直线的解析式为
所在直线的解析式为![]() ,曲线解析式为
,曲线解析式为![]() ,
,
解得![]() 点坐标为
点坐标为![]() ,
,![]() 为
为![]() .
.
∴![]() .
.
(3)解:直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 的横坐标满足
的横坐标满足![]() .
.
解得![]() (舍去负解).∴
(舍去负解).∴![]() 点坐标
点坐标![]() .
.
又∵曲线![]() 与
与![]() 的交点
的交点![]() 坐标为
坐标为![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
解得![]() .(舍去
.(舍去![]() )
)

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目