题目内容
【题目】如图，在四边形ABCD中，AB∥CD，∠1=∠2，DB=DC．
（1）求证：△ABD≌△EDC；
（2）若∠A=135°，∠BDC=30°，求∠BCE的度数．
【答案】（1）证明见解析；（2）60°．
【解析】试题分析：由全等三角形的判定方法：ASA，即可证明：△ABD≌△EDC；
（2）根据三角形内角和定理可求出∠1的度数，进而可得到∠2的度数，再根据△BDC是等腰三角形，即可求出∠BCE的度数．
试题解析：（1）证明：∵AB∥CD，∴∠ABD=∠EDC，
在△ABD和△EDC中，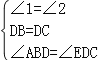
， ∴△ABD≌△EDC（ASA），
（2）解：∵∠ABD=∠EDC=30°，∠A=135°， ∴∠1=∠2=15°， ∵DB=DC，
∴∠DCB=(180°－∠DBC)=75°， ∴∠BCE=75°﹣15°=60°．
仁爱英语同步练习册系列答案
学习实践园地系列答案【题目】随着地铁和共享单车的发展，“地铁
单车”已成为很多市民出行的选择，李华从学院路站出发，先乘坐地铁，准备在离家较近的
， 
， 
， 
， 
中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与学院路距离为
（单位：千米），乘坐地铁的时间
(单位：分钟)是关于
的一次函数，其关系如下表：
地铁站 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（
）求
关于
的函数表达式．
（
）李华骑单车的时间
(单位：分钟)与
的关系式为
，求李华从学院路站回到家的最短总时间，并指出他在哪一站出地铁．
【题目】某校八（1）班同学为了解2018年姜堰某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：
月均用水量x（t） | 频数（户） | 频率 |
0＜x≤5 | 6 | 0.12 |
5＜x≤10 | 12 | 0.24 |
10＜x≤15 | m | 0.32 |
15＜x≤20 | 10 | n |
20＜x≤25 | 4 | 0.08 |
25＜x≤30 | 2 | 0.04 |
（1）本次调查采用的调杳方式是 （填“普査”或“抽样调查”），样本容量是 ；
（2）补全频数分布直方图：
（3）若将月均用水量的频数绘成扇形统计图，则月均用水量“15＜x≤20”的圆心角度数是 ；
（4）若该小区有5000户家庭，求该小区月均用水量超过20t的家庭大约有多少户？
