Question

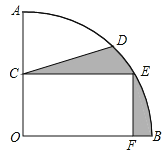
【题目】如图，在扇形中，，是的中点，是的中点，点在上，点在上，四边形是矩形，连接．若，则阴影部分的面积为____________．（结果保留）

Answer 1

【答案】

【解析】

连接OD、OE，作DH⊥OA于H，根据D是的中点可得∠AOD=∠BOD=45°，继而可得△HDO为等腰直角三角形，求出DH，即可求得△COD的面积和扇形BOD的面积，最后根据S阴影=S△COD+S扇形DOB-S矩形OCEF即可求出阴影部分的面积．

如图，连接OD，作DH⊥OA于H，

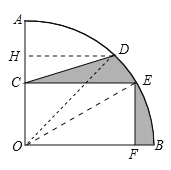
∵D是的中点，

∴∠AOD=∠BOD，

∵∠AOB=90°，

∴∠AOD=∠BOD=45°，

∴，

∵点C为OA的中点，

∴，

∴，

∴，S扇形BOD=，S矩形OCEF=OCCE=，

∴S阴影=S△COD+S扇形DOB-S矩形OCEF=，

故答案为：．