题目内容
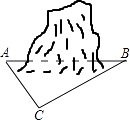
【题目】如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=![]() ,那么AC的长等于__________ .
,那么AC的长等于__________ .

【答案】7
【解析】如图,在AC上截取CF=AB,
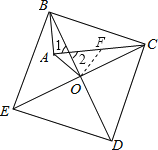
∵四边形BCDE是正方形,
∴OB=OC,∠BOC=90°
∴∠2+∠OCF=90°.
∵∠BAC=90°,
∴∠1+∠OBA=90°.
∵∠1=∠2(对顶角相等),
∴∠OBA=∠OCF.
在△ABO和△FCO中,
∵OB=OC,
∠OBA=∠OCA,
CF=AB,
∴△ABO≌△FCO(ASA),
.∴OF=AO=![]() ,∠AOB=∠FOC,
,∠AOB=∠FOC,
∴∠AOF=∠AOB+∠BOF=∠FOC+∠BOF=∠BOC=90°,
∴△AOF是等腰直角三角形,
![]() ,
,
∴AC=AF+CF=4+3=7.
故答案为:7.
点睛:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理等知识,解题的关键是添加辅助线构造全等三角形.

练习册系列答案
相关题目