题目内容
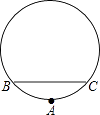
【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA. 
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
【答案】
(1)解:线段AC是⊙O的切线;
理由如下:∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换);
又∵OA=OB(⊙O的半径),
∴∠B=∠OAB(等边对等角);
∵OB⊥OC(已知),
∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,
∴线段AC是⊙O的切线

(2)解:设AC=x(x>0).
∵∠CAD=∠CDA(已知),
∴DC=AC=x(等角对等边);
∵OA=5,OD=1,
∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,
OC2=AC2+OA2,即
(1+x)2=x2+52,
解得x=12,即AC=12.
【解析】(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°.所以线段AC是⊙O的切线;(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在Rt△OAC中,根据勾股定理来求AC的长度.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目