题目内容
如图1,在△ABC中,点D为BC边中点,直线a绕顶点A旋转,若点B、D在直线a的异侧,BE⊥直线a于点E,CF⊥直线a于点F,连接DE、DF.
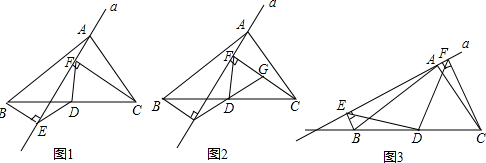
(1)延长ED交CF于点G(如图2).①求证:△BDE≌△CDG;②DE=DF;
(2)若直线a绕点A旋转到(图3)的位置时,点B、D在直线a的同侧,其它条件不变,此时DE=DF成立吗?若成立,请给予证明,若不成立,请说明理由.

(1)延长ED交CF于点G(如图2).①求证:△BDE≌△CDG;②DE=DF;
(2)若直线a绕点A旋转到(图3)的位置时,点B、D在直线a的同侧,其它条件不变,此时DE=DF成立吗?若成立,请给予证明,若不成立,请说明理由.
分析:(1)①由BE⊥直线a于点E,CF⊥直线a就可以得出BE∥CF,就可以得出∠EBD=∠GCD,∠DEB=∠DGC,就可以由得出AAS得出△BDE≌△CDG;
②由△BDE≌△CDG就可以得出DE=DG,由直角三角形的性质就可以得出结论;
(2)延长ED交FC的延长线于点G,根据条件可以得出证明△BDE≌△CDG就可以得出ED=DG,由直角三角形的性质就可以得出结论.
②由△BDE≌△CDG就可以得出DE=DG,由直角三角形的性质就可以得出结论;
(2)延长ED交FC的延长线于点G,根据条件可以得出证明△BDE≌△CDG就可以得出ED=DG,由直角三角形的性质就可以得出结论.
解答:解:(1)①∵BE⊥直线a,CF⊥直线a,
∴BE∥CF,
∴∠EBD=∠GCD,∠DEB=∠DGC.
∵点D为BC边中点,
∴BD=CD.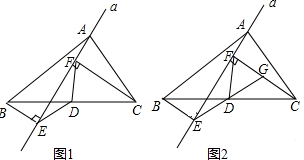
在△BDE和△CDG中,
,
∴△BDE≌△CDG(AAS);
②∵△BDE≌△CDG,
∴ED=GD.
∵CF⊥直线a,
∴∠CFE=90°,
∴DF=
EG.
∴DE=DF;
(2)DE=DF成立
理由:延长ED交FC的延长线于点G,
①∵BE⊥直线a,CF⊥直线a,
∴BE∥CF,
∴∠EBD=∠GCD,∠DEB=∠DGC.
∵点D为BC边中点,
∴BD=CD.
在△BDE和△CDG中,
,
∴△BDE≌△CDG(AAS);
∴ED=GD.
∵CF⊥直线a,
∴∠CFE=90°,
∴DF=
EG.
∴DE=DF.
∴BE∥CF,
∴∠EBD=∠GCD,∠DEB=∠DGC.
∵点D为BC边中点,
∴BD=CD.

在△BDE和△CDG中,
|
∴△BDE≌△CDG(AAS);
②∵△BDE≌△CDG,
∴ED=GD.
∵CF⊥直线a,
∴∠CFE=90°,
∴DF=
| 1 |
| 2 |
∴DE=DF;
(2)DE=DF成立
理由:延长ED交FC的延长线于点G,
①∵BE⊥直线a,CF⊥直线a,
∴BE∥CF,
∴∠EBD=∠GCD,∠DEB=∠DGC.
∵点D为BC边中点,
∴BD=CD.
在△BDE和△CDG中,
|

∴△BDE≌△CDG(AAS);
∴ED=GD.
∵CF⊥直线a,
∴∠CFE=90°,
∴DF=
| 1 |
| 2 |
∴DE=DF.
点评:本题考查了直角三角形的斜边上的中线的性质的运用,全都三角形的判定及性质的运用,平行线的性质的运用,解答时证明三角形的全等是关键.

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=