题目内容
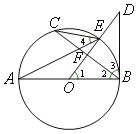
【题目】如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
【答案】(1)答:BD和⊙O相切.
证明:∵OD⊥BC,
∴∠OFB=∠BFD =90°,
∴∠D+∠3=90°.
∵∠4=∠D=∠2, ……………………………1分
∴∠2+∠3=90°,
∴∠OBD=90°,
即OB⊥BD.
∵点B在⊙O上,
∴BD和⊙O相切. ……………………………2分
(2) ∵OD⊥BC,BC=8,
∴BF="FC=4. " ……………………………3分
∵ AB=10,
∴OB=OA=5.
在Rt△OFB中, ∠OFB =90°,
∵OB=5,BF=4,
∴OF="3. " ……………………………4分
∴tan∠1=![]() .
.
在Rt△OBD中, ∠OBD =90°,
∵tan∠1=![]() , OB=5,
, OB=5,
∴![]() . …………………………… 5分
. …………………………… 5分
【解析】试题分析:(1)因为同弧所对的圆周角相等,所以有∠AEC=∠ABC,又∠AEC=∠ODB,所以∠ABC=∠ODB,OD⊥弦BC,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.
(2)连接AC,由于AB为直径,所以AC和BC垂直,又由(1)知∠ABC=∠ODB,所以有△ACB∽△OBD,而AC可由勾股定理求出,所以根据对应线段成比例求出BD.
试题解析:(1)答:BD和⊙O相切.
证明:∵OD⊥BC,
∴∠OFB=∠BFD=90°,
∴∠D+∠3=90°.
∵∠4=∠D=∠2,
∴∠2+∠3=90°,
∴∠OBD=90°,
即OB⊥BD.
∵点B在⊙O上,
∴BD和⊙O相切.
(2)∵OD⊥BC,BC=8,
∴BF="FC=4"
∵AB=10,
∴OB=OA=5.
在Rt△OFB中, ∠OFB =90°,
∵OB=5,BF=4,
∴OF=3.
∴tan∠1=![]() .
.
在Rt△OBD中, ∠OBD =90°,
∵tan∠1=![]() , OB=5,
, OB=5,
∴![]() .
.