题目内容
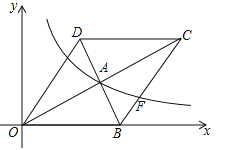
【题目】已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
求证:AD平分∠BAC,填写分析和证明中的空白.

证明:∵AD⊥BC,EF⊥BC(已知)
∴______∥______(______)
∴______=______(两直线平行,内错角相等)
______=______(两直线平行,同位角相等)
∵______(已知),∴______
即AD平分∠BAC(______)
【答案】AD,EF,垂直于同一条直线的两条直线平行,∠BAD,∠1,∠CAD,∠2,∠1=∠2,∠BAD=∠CAD,角平分线定义.
【解析】
根据平行线的判定推出AD∥EF,根据平行线的性质得出∠BAD=∠1,∠CAD=∠2,推出∠BAD=∠CAD即可.
证明:∵AD⊥BC,EF⊥BC(已知),
∴AD∥EF(垂直于同一直线的两直线平行),
∴∠BAD=∠1(两直线平行,内错角相等),
∠CAD=∠2(两直线平行,同位角相等),
∵∠1=∠2,
∴∠BAD=∠CAD,
即AD平分∠BAC(角平分线定义),
故答案为:AD,EF,垂直于同一条直线的两条直线平行,∠BAD,∠1,∠CAD,∠2,∠1=∠2,∠BAD=∠CAD,角平分线定义.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】李克强总理说:”一个国家养成全民阅读习惯非常重要…我希望全民阅读能够形成一种氛围,无处不在.“为了响应国家的号召,某”希望“学校的全体师生掀起了阅读的热潮.下面是该校三个年级的学生人数分布扇形统计图与学生在4月份阅读课外书籍人次的统计图表,其中七年级的学生人数为240人.请解答下列问题:
图书种类 | 频数 | 频率 |
科普书籍 | A | B |
文学 | 1200 | C |
漫画丛书 | D | 0.35 |
其他 | 200 | 0.05 |
(1)该校七年级学生人数所在扇形的圆心角为______°,该校的学生总人数为______人;
(2)请补全条形统计图;
(3)为了鼓励学生读书,学校决定在“五四”青年节举行两场读书报告会.报告会的内容从“科普书籍”“文学”“漫画丛书”“其他”中任选两个.用画树状图或列表的方法求两场报告会的内容恰好是“科普书籍”与“漫画丛书”的概率.(“科普书籍”“文学”“漫画丛书”“其他”,可以分别用K,W,M,Q来表示)