ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕуPЮЊ
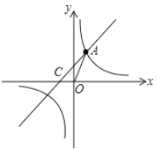
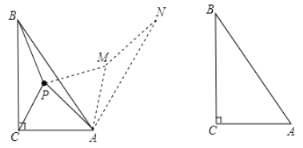
ЃЌЕуPЮЊ![]() ФквЛЕуЃЌСЌНгPAЃЌPBЃЌPCЃЌЧѓPA+PB+PCЕФзюаЁжЕЃЌаЁЛЊЕФНтЬтЫМТЗЃЌвдЕуAЮЊа§зЊжааФЃЌНЋ
ФквЛЕуЃЌСЌНгPAЃЌPBЃЌPCЃЌЧѓPA+PB+PCЕФзюаЁжЕЃЌаЁЛЊЕФНтЬтЫМТЗЃЌвдЕуAЮЊа§зЊжааФЃЌНЋ![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌФЧУДОЭНЋЧѓPA+PB+PCЕФжЕзЊЛЏЮЊЧѓPM+MN+PCЕФжЕЃЌСЌНгCNЃЌЕБЕуPЃЌMТфдкCNЩЯЪБЃЌДЫЬтПЩНтЃЎ
ЃЌФЧУДОЭНЋЧѓPA+PB+PCЕФжЕзЊЛЏЮЊЧѓPM+MN+PCЕФжЕЃЌСЌНгCNЃЌЕБЕуPЃЌMТфдкCNЩЯЪБЃЌДЫЬтПЩНтЃЎ
ЃЈ1ЃЉЧыХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧыФуВЮПМаЁЛЊЕФНтЬтЫМТЗЃЌжЄУїPA+PB+PC=PM+MN+PCЃЛ
ЃЈ3ЃЉЕБ![]() ЃЌЧѓPA+PB+PCЕФзюаЁжЕЃЎ
ЃЌЧѓPA+PB+PCЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕШБпШ§НЧаЮЃЌМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОна§зЊЕФаджЪПЩвдЕУГі![]() ЃЌМДПЩжЄУїГі
ЃЌМДПЩжЄУїГі![]() ЪЧЕШБпШ§НЧаЮЃЛ
ЪЧЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉ![]() ШЦЕуAЫГЪБеыа§зЊ
ШЦЕуAЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌИљОнЕФа§зЊЕФаджЪЕУЕН
ЃЌИљОнЕФа§зЊЕФаджЪЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌЯрМгМДПЩЕУ
ЃЌЯрМгМДПЩЕУ![]() ЃЛ
ЃЛ
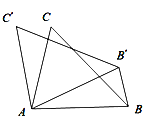
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊ![]() ЃЌЕБCЁЂPЁЂMЁЂNЫФЕуЙВЯпЪБЃЌPA+PB+PCШЁЕНзюаЁЃЌгЩ
ЃЌЕБCЁЂPЁЂMЁЂNЫФЕуЙВЯпЪБЃЌPA+PB+PCШЁЕНзюаЁЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУCNДЙжБЦНЗжABЃЌдйРћгУжБНЧШ§НЧаЮЕФБпНЧЙиЯЕЃЌДгЖјЧѓГіPA+PB+PCЕФзюаЁжЕЃЎ
ЃЌПЩЕУCNДЙжБЦНЗжABЃЌдйРћгУжБНЧШ§НЧаЮЕФБпНЧЙиЯЕЃЌДгЖјЧѓГіPA+PB+PCЕФзюаЁжЕЃЎ
ЃЈ1ЃЉЕШБпШ§НЧаЮЃЛ
![]() ШЦAЕуЫГЪБеыа§зЊ
ШЦAЕуЫГЪБеыа§зЊ![]() ЕУЕНMAЃЌ
ЕУЕНMAЃЌ
![]() ЃЌ
ЃЌ
![]() ЪЧЕШБпШ§НЧаЮ.
ЪЧЕШБпШ§НЧаЮ.
ЃЈ2ЃЉ![]() ШЦЕуAЫГЪБеыа§зЊ
ШЦЕуAЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌ
ЃЌ
![]() ЃЌгЩЃЈ1ЃЉПЩжЊ
ЃЌгЩЃЈ1ЃЉПЩжЊ![]() ЃЌ
ЃЌ
![]() .
.
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊ![]() ЃЌЕБCЁЂPЁЂMЁЂNЫФЕуЙВЯпЪБЃЌPA+PB+PCШЁЕНзюаЁЃЎ
ЃЌЕБCЁЂPЁЂMЁЂNЫФЕуЙВЯпЪБЃЌPA+PB+PCШЁЕНзюаЁЃЎ
СЌНгBNЃЌ
гЩа§зЊЕФаджЪПЩЕУЃКAB=ANЃЌЁЯBAM=60Ёу
Ёр![]() ЪЧЕШБпШ§НЧаЮЃЛ
ЪЧЕШБпШ§НЧаЮЃЛ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЪЧABЕФДЙжБЦНЗжЯпЃЌДЙзуЮЊЕуQЃЌ
ЪЧABЕФДЙжБЦНЗжЯпЃЌДЙзуЮЊЕуQЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() .
.

 УћаЃПЮЬУЯЕСаД№АИ
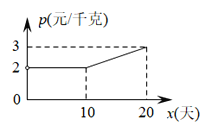
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПМзЁЂввСНУћЖгдБВЮМгЩфЛїбЕСЗЃЌУПШЫЩфЛї10ДЮЃЌГЩМЈЗжБ№ШчЯТЃК

ИљОнвдЩЯаХЯЂЃЌећРэЗжЮіЪ§ОнШчЯТЃК
ЦНОљГЩМЈ/ЛЗ | жаЮЛЪ§/ЛЗ | жкЪ§/ЛЗ | ЗНВю | |
Мз | a | 7 | 7 | 1.2 |
вв | 7 | b | 8 | c |
ЃЈ1ЃЉaЃН_____ЃЛbЃН_____ЃЛcЃН_____ЃЛ
ЃЈ2ЃЉЬюПеЃКЃЈЬюЁАМзЁБЛђЁАввЁБЃЉЃЎ
ЂйДгЦНОљЪ§КЭжаЮЛЪ§ЕФНЧЖШРДБШНЯЃЌГЩМЈНЯКУЕФЪЧ_____ЃЛ
ЂкДгЦНОљЪ§КЭжкЪ§ЕФНЧЖШРДБШНЯЃЌГЩМЈНЯКУЕФЪЧ_____ЃЛ
ЂлГЩМЈЯрЖдНЯЮШЖЈЕФЪЧ_____ЃЎ