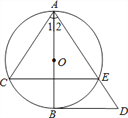
题目内容
【题目】如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.
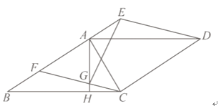
(1)若AE=2,CD=5,则△BCF的面积为 ;△BCF的周长为 ;
(2)求证:BC=AG+EG.
【答案】(1)3,![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据平行和垂直的特点求出BF,AF,再根据勾股定理求出CD,根据FP与BA的比值求出面积,再根据勾股定理求CF,BC即可得到周长.
(2)在AD上截取AM=AG,连接CM,证△FAG≌△CAM;证△EFG≌△DCM.
解:(1)面积为3;周长为![]()
∵四边形ABCD和四边形CDEF都是平行四边形,
∴EF=CD,AB=CD,AB∥CD
∴EF=AB=CD=5
∴AE=EF-AE=5-2=3
∴BF=5-3=2
过F作FP⊥BC
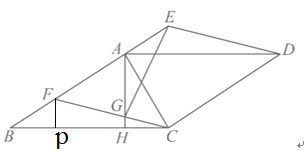
则FP:AH=BF:AB=2:5,
∴![]() ,
,
∵AC⊥CD,AB∥CD,
∴AB⊥AC,即∠BAC=90°,
∵AC=AF=3,
∴CF=![]() ,BC=
,BC=![]() ,
,
∴![]()
∴△BCF的面积为3,△BCF周长为![]()
(2)在AD上截取AM=AG,连接CM,
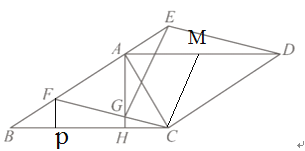
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵AH⊥BC
∴AD⊥AH
∴∠DAH=90°
∵∠BAC=90°
∴∠DAH=∠BAC
∴∠DAH-∠CAH =∠BAC-∠CAH
∴∠BAH=∠CAD
∵AF=AC
∴△FAG≌△CAM
∴FG=CM,∠ACM=∠AFG
∵四边形CDEF是平行四边形,
∴EF∥CD,EF=CD,
∴∠DCF+∠AFC=180°,
∵AF=AC, ∠BAC=90°,
∴∠AFC=∠ACF=45°,
∴∠DCF=180°-∠AFC=135°,
∴∠ACM=∠AFG=45°,
∴∠DCM=∠FCD-∠ACF-∠ACM=45°,
∴∠AFG=∠DCM,
∴△EFG≌△DCM,
∴EG=DM,
∵AD=AM+DM,
∴AD=AG+EG,
∵AD=BC,
∴BC=AG+EG.

 阅读快车系列答案
阅读快车系列答案