题目内容
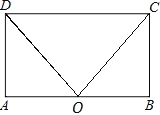
【题目】如图,在平行四边形ABCD中,点O是AB的中点,且OC=OD.
(1)求证:平行四边形ABCD是矩形;
(2)若AD=3,∠COD=60°,求矩形ABCD的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据平行四边形的性质,得出AD=BC,AD∥BC,求出∠A+∠B=180°,根据全等三角形的判定△DAO≌△CBO,根据全等三角形的性质∠A=∠B,求出∠A=90°,根据矩形的判定得出即可;
(2)根据全等求出∠DOA=∠COB,根据勾股定理得出:![]() 求出AO,在球场AB,即可求出面积.
求出AO,在球场AB,即可求出面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠A+∠B=180°,
∵O是AB的中点,
∴AO=BO,
在△DAO和△CBO中
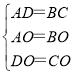
∴△DAO≌△CBO(SSS),
∴∠A=∠B,
∵∠A+∠B=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
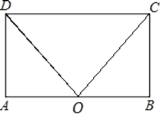
(2)解:∵△DAO≌△CBO,∠DOC=60°,
∴∠DOA=∠COB=![]() (180°-∠DOC)=60°,
(180°-∠DOC)=60°,
∵∠A=90°,
∴∠ADO=30°,
![]() DO=2AO,
DO=2AO,
∵AD=3,
由勾股定理得:![]()
解得:AO=![]() , ∴AB=2AO=
, ∴AB=2AO=![]() ,
,
∴ABCD的面积是AB×AD=![]()

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目