题目内容
已知：如图，在⊿ABC中，∠ACB=90°，D、E、F分别是AC、AB、BC的中点。求证：CF=DE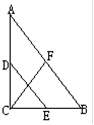
见解析
证明：∵在Rt⊿ABC中，F是斜边AB的中点
∴
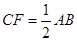
∵D、E分别是AC、BC的中点
∴DE是三角形ABC的中位线
∴
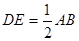
∴DE=CF
由于△ABC中，∠ACB=90°，D、E、F分别是AC、AB、BC的中点．故CF=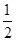
AB，DE是△ABC的中位线，故DE= 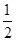AB，所以CF=DE
∴
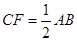
∵D、E分别是AC、BC的中点
∴DE是三角形ABC的中位线
∴
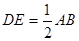
∴DE=CF
由于△ABC中，∠ACB=90°，D、E、F分别是AC、AB、BC的中点．故CF=
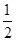AB，DE是△ABC的中位线，故DE= 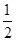AB，所以CF=DE
练习册系列答案
相关题目
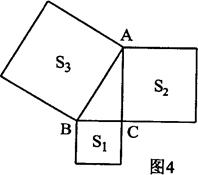
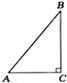
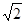≈1.414，
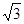≈1.732）
