题目内容
阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2＝a4－b4，试判断△ABC的形状。
解：∵ a2c2－b2c2＝a4－b4， ①
∴ c2（a2－b2）＝（a2 + b2）（a2－b2）， ②
∴ c2＝ a2+b2， ③
∴ △ABC为直角三角形。
问：
小题1:上述解题过程，从哪一步开始出现错误？请写出该步的代号 ；
小题2:该步正确的写法应是
小题3:本题正确的结论应是
解：∵ a2c2－b2c2＝a4－b4， ①
∴ c2（a2－b2）＝（a2 + b2）（a2－b2）， ②
∴ c2＝ a2+b2， ③
∴ △ABC为直角三角形。
问：
小题1:上述解题过程，从哪一步开始出现错误？请写出该步的代号 ；
小题2:该步正确的写法应是
小题3:本题正确的结论应是
小题1:③
小题2:忽略了a2- b2=0的可能
小题3:△ABC是等腰三角形或直角三角形或等腰直角三角形
：（ⅰ）③；
（ⅱ）忽略了a2- b2=0的可能；
（ⅲ）接第③步：
∵c2（a2- b2）=（a2- b2）（a2+ b2），
∴c2（a2- b2）-（a2- b2）（a2+ b2）=0，
∴（a2- b2）[c2-（a2+ b2）]=0，
∴a2- b2=0或c2-（a2+ b2）=0．故a=b或c2= a2+ b2，
∴△ABC是等腰三角形或直角三角形或等腰直角三角形
（ⅱ）忽略了a2- b2=0的可能；
（ⅲ）接第③步：
∵c2（a2- b2）=（a2- b2）（a2+ b2），
∴c2（a2- b2）-（a2- b2）（a2+ b2）=0，
∴（a2- b2）[c2-（a2+ b2）]=0，
∴a2- b2=0或c2-（a2+ b2）=0．故a=b或c2= a2+ b2，
∴△ABC是等腰三角形或直角三角形或等腰直角三角形
练习册系列答案
相关题目
cos∠ABC= 
如图放置，点A，B，C都在格点上，则sin∠BAC的值为 ( )
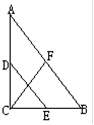
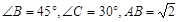；求AC的长．
﹥300时，则
的值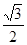 
。（填“＞”“＜”“＝”）