题目内容
【题目】(1)解不等式![]()
(2)解不等式组:并将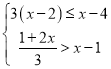 其解集表示在如图所示的数轴上
其解集表示在如图所示的数轴上
![]()
(3) ,并写出不等式组的整数解.
,并写出不等式组的整数解.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;整数解为-1,0,1,2,3
;整数解为-1,0,1,2,3
【解析】
(1)不等式去括号、移项合并、系数化为1即可求出不等式的解集;
(2)解第一个不等式得x≤1,解第二个不等式得x<4,然后根据小小取小得到不等式组的解集.再在数轴上表示出不等式的解集即可.
(3) 将不等式组中的不等式分别记作①和②,分别求出不等式①和②的解集,找出两解集的公共部分,确定出不等式组的解集,在不等式组解集中找出满足范围的整数,即可得到原不等式组的整数解;
解:(1)![]()
去括号 2x+2-1≥3x+2
移项 2x-3x≥2-2+1
合并同类项,系数化为1得 x≤-1
(2)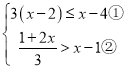
由![]() 得 x≤1
得 x≤1
由![]() x<4
x<4
所以不等式组的解集为: x≤1.
其解集表示在数轴上如下:
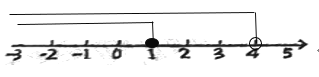
(3)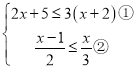
由![]() 得 x≥-1
得 x≥-1
由![]() x≤3
x≤3
所以不等式组的解集为:-1≤ x≤3.
所以这个不等式组的整数解为:-1、0、1、2、3.
故答案为(1)![]() ;(2)
;(2)![]() ;(3)整数解为-1,0,1,2,3.
;(3)整数解为-1,0,1,2,3.

练习册系列答案
相关题目