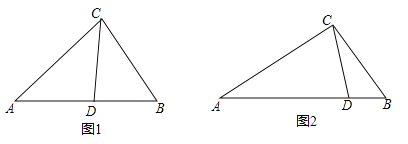Question

【题目】如图1，在平面直角坐标系中，直线:与轴相交于B，与轴相交于点A.直线:经过原点，并且与直线相交于C点.

(1)求ΔOBC的面积；

(2)如图2，在轴上有一动点E，连接CE.问CE+BE是否有最小值，如果有，求出相应的点E的坐标及CE+BE的最小值；如果没有，请说明理由；

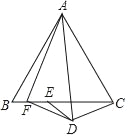
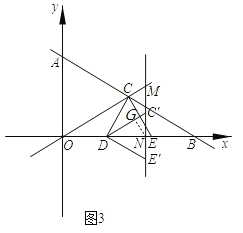
(3)如图3，在(2)的条件下，以CE为一边作等边ΔCDE，D点正好落在轴上.将ΔDCE绕点D顺时针旋转，旋转角度为(0°≤≤360)，记旋转后的三角形为ΔDCE′，点C，E的对称点分别为C′，E′.在旋转过程中，设C′E′所在的直线与直线相交于点M，与轴正半轴相交于点N.当ΔOMN为等腰三角形时，求线段ON的长?

Answer 1

【答案】(1) ；(2)E（6，0），最小值为.(3) ON＝或3-或6或33或3+3.

【解析】

（1）求出点B、C的坐标，就可以求出△OBC的面积；
（2）作点C关于x轴的对称点P，作射线BP，过点C作CH⊥BP交x轴于点E，则CE+BE有最小值；
（3）分两种情况：∠MON为等腰三角形的顶角或底角．

（1）如图1，易求点B（9，0），解方程组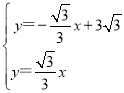 得： ；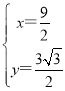
故点C（，），
∴S△OBC=×9×=．
（2）如图2，作点C关于x轴的对称点P，作射线BP，过点E作EH⊥BP于点H，取BE中点I，连接HI．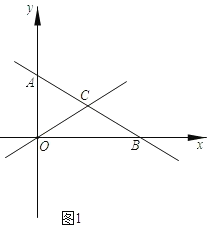

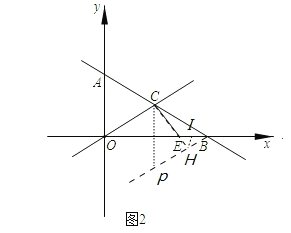
易知：∠BOC=∠OBC=∠OBP=30°，∠BHE=90°，
∵IE=IB，
∴IH=IE=IB
∵∠BEH=60°，
∴△EIH是等边三角形，
∴EH=EI=EB，
∴当C、E、H三点共线且CH⊥BP时，CH的长度最小，即CE+BE有最小值；

∵OC=CB=3，∠BCH=30°，∠BHC=90°，
∴BH=BC=
∴CH=
=
故CE+BE有最小值为．
在Rt△BEH中，∵∠EBH=30°，
∴EH=BE，
∵BE2-EH2=BH2
∴BE=3
∴E（6，0）．
（3）△OMN为等腰三角形，分三种情况：
①当∠OMN=∠ONM时，
∵∠MON=30°，

∴∠OMN=∠ONM=75°
如图3，当∠OMN=∠ONM=75°时，∠C′DN=45°，∠DC′N=60°，
∴∠CDC′=α=15°，过点N作NG⊥DC′于G，
可求得GC′= ，
∴ON＝
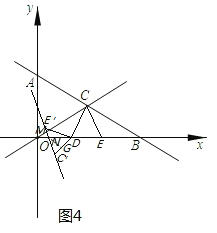
如图4，当∠OMN=∠ONM=75°时，∠C′DN=45°，旋转角α=195°
过点N作NG⊥DC′于G，
可求得DN=，
∴ON=3-，
②如图5，当∠OMN=∠MON=30°时，∠ONM=120°，
此时旋转角α=60°，易得ON=6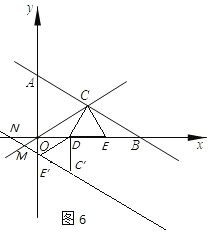

③如图6，图7，当∠ONM=∠NOM=30°时，
∴∠OMN=120°，
∵∠DE′C′=60°，α=150°或330°，
∴DE′∥OM，
过点E′作E′G⊥x轴于G，可求得DN=3，
∴ON＝33或3
综上所述，ON＝或3-或6或33或3+3.