题目内容
【题目】平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.
(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;
(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;
(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.



【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)证明△OAF≌△BOP(ASA),得出OF=PB=3,则P点坐标可求出;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用
,利用![]() ,
,![]() 证得四边形
证得四边形![]() 为平行四边形,然后根据直角三角形斜边中线等于斜边的一半求得MN=AN,用HL定理证明
为平行四边形,然后根据直角三角形斜边中线等于斜边的一半求得MN=AN,用HL定理证明![]() ,从而求得
,从而求得![]() 为
为![]() 的垂直平分线,使问题得解;
的垂直平分线,使问题得解;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由矩形和正方形的性质求得
,由矩形和正方形的性质求得![]() 为等腰直角三角形,从而求得
为等腰直角三角形,从而求得![]() ,
,![]() ,利用垂直平分线的性质求得ON=NP,然后根据HL定理证得
,利用垂直平分线的性质求得ON=NP,然后根据HL定理证得![]() ,然后利用全等三角形的性质求得
,然后利用全等三角形的性质求得![]() ,即
,即![]() 为等腰直角三角形,从而使问题得解.
为等腰直角三角形,从而使问题得解.
解:∵A(0,8),
∴OA=8,
∵EF⊥OP于M,
∴∠OMF=90°,
∴∠MOF+∠OFM=90°,
∵∠OFM+∠OAF=90°,
∴∠MOF=∠OAF.
∵OA=OB,∠AOF=∠OBP,
∴△OAF≌△BOP(ASA),
∴OF=PB=3,
∴P(8,3);

(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
∵在正方形AOBC中,OA=BC=AC,且点P为BC中点
∴![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵EF⊥OP
∴![]()
又∵N为OA中点
∴在Rt△AOM中,MN=AN
在Rt△AHN和Rt△MHN中,MN=AN,NH=NH
∴![]()
∴![]() ,
,![]() 为
为![]() 的垂直平分线
的垂直平分线
∴![]()

(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
由题意可知四边形AHGC是矩形且四边形AOBC为正方形
∴HG=AC=OA
在正方形AOBC中,∠OAB=45°
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,![]()
由EF⊥OP于M且M为OP的中点
∴MN垂直平分OP
∴ON=NP
在Rt△ONH和Rt△NPG中![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() .
.


【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
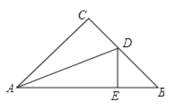
A. 4cm B. 6cm C. 8cm D. 10cm
【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.





