题目内容
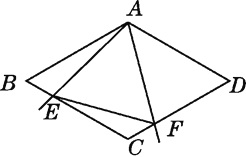
【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.
【答案】13![]() .
.
【解析】
作辅助线,构建直角三角形,先求CE的长,从而得FM和AM的长,根据勾股定理可得AF的长.
解:过D作DH⊥BC于H,
∵DC=DE=10,
∴EH=HC,
∵∠CDE=120°,
∴∠DCH=30°,
∴CH=EH=5![]() ,
,
∴CE=10![]() ,
,
∴BE=BC﹣CE=24﹣10![]() ,
,
∵F是BE的中点,
∴BF=![]() =12﹣5
=12﹣5![]() ,
,
过A作AM⊥BC于M,
∵△ABC是等边三角形,
∴BM=![]() BC=12,AM=12
BC=12,AM=12![]() ,
,
∴FM=BM﹣BF=12﹣(12﹣5![]() )=5
)=5![]() ,
,
由勾股定理得:AF=![]() =
=![]() =13
=13![]() .
.
故答案为:13![]() .
.

练习册系列答案
相关题目
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
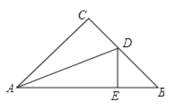
A. 4cm B. 6cm C. 8cm D. 10cm
【题目】为了了解七年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°,根据图表中提供的信息,回答下列问题:
体育成绩统计表 | ||
体育成绩(分) | 人数(人) | 百分比(%) |
26 | 8 | 16 |
27 | 12 | 24 |
28 | 15 | |
29 | n | |
30 | ||
(1)求样本容量及n的值;
(2)已知该校七年级共有500名学生,如果体育成绩达28分以上为优秀,请估计该校七年级学生体育成绩达到优秀的总人数.