题目内容
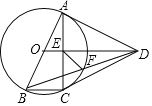
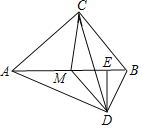
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点M是斜边AB的中点,MD∥BC,且MD=CM,DE⊥AB于点E,连结AD、CD.
(1)求证:△MED∽△BCA;
(2)求证:△AMD≌△CMD;
(3)设△MDE的面积为S1,四边形BCMD的面积为S2,当S2=![]() S1时,求cos∠ABC的值.
S1时,求cos∠ABC的值.
【答案】(1)证明见解析;(2)证明见解析;(3)cos∠ABC=![]() .
.
【解析】
(1)易证∠DME=∠CBA,∠ACB=∠MED=90°,从而可证明△MED∽△BCA;
(2)由∠ACB=90°,点M是斜边AB的中点,可知MB=MC=AM,从而可证明∠AMD=∠CMD,从而可利用全等三角形的判定证明△AMD≌△CMD;
(3)易证MD=2AB,由(1)可知:△MED∽△BCA,所以![]() ,所以S△MCB=
,所以S△MCB=![]() S△ACB=2S1,从而可求出S△EBD=S2﹣S△MCB﹣S1=
S△ACB=2S1,从而可求出S△EBD=S2﹣S△MCB﹣S1=![]() S1,由于
S1,由于![]() ,从而可知
,从而可知![]() ,设ME=5x,EB=2x,从而可求出AB=14x,BC=
,设ME=5x,EB=2x,从而可求出AB=14x,BC=![]() ,最后根据锐角三角函数的定义即可求出答案.
,最后根据锐角三角函数的定义即可求出答案.
(1)∵MD∥BC,
∴∠DME=∠CBA,
∵∠ACB=∠MED=90°,
∴△MED∽△BCA;
(2)∵∠ACB=90°,点M是斜边AB的中点,
∴MB=MC=AM,
∴∠MCB=∠MBC,
∵∠DMB=∠MBC,
∴∠MCB=∠DMB=∠MBC,
∵∠AMD=180°﹣∠DMB,
∠CMD=180°﹣∠MCB﹣∠MBC+∠DMB=180°﹣∠MBC,
∴∠AMD=∠CMD,
在△AMD与△CMD中,
 ,
,
∴△AMD≌△CMD(SAS);
(3)∵MD=CM,
∴AM=MC=MD=MB,
∴MD=2AB,
由(1)可知:△MED∽△BCA,
∴![]() ,
,
∴S△ACB=4S1,
∵CM是△ACB的中线,
∴S△MCB=![]() S△ACB=2S1,
S△ACB=2S1,
∴S△EBD=S2﹣S△MCB﹣S1=![]() S1,
S1,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设ME=5x,EB=2x,
∴MB=7x,
∴AB=2MB=14x,
∵![]() ,
,
∴BC=10x,
∴cos∠ABC=![]() .
.

 阅读快车系列答案
阅读快车系列答案