Question

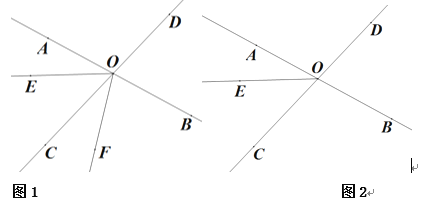
【题目】如图，直线AB、CD相交于点O．已知∠BOD=75°，OE把∠AOC分成两个角，且∠AOE=∠EOC

（1）求∠AOE的度数；

（2）将射线OE绕点O逆时针旋转°（0°＜α＜360°）到OF．

①如图2，当OF平分∠BOE时，求∠DOF的度数；

②若∠AOF=120°时，直接写出的度数.

Answer 1

【答案】（1）∠AOE=30°（2）①∠DOF=150° ②

【解析】（1）根据对顶角相等求出∠BAOC的度数，设∠AOE=2x，根据题意列出方程，解方程即可；

（2）①根据角平分线的定义求出∠BOF的度数即可；

②根据∠AOF=120°画出图形，根据角的和与差即可求解．

解：（1）∵∠AOE=∠EOC，

∴设∠AOE=2x，则∠EOC=3x，

∴∠AOC=5x，

∵∠AOC=∠BOD=75°，

∴5x=75°，

解得：x=15°，

则2x=30°，

∴∠AOE=30°；

（2）①∵∠AOE=30°，

∴∠BOE=180°∠AOE=150°，

∵OF平分∠BOE，

∴∠BOF=75°，

∵∠BOD=75°，

∴∠DOF=150°，

②有两种情况：

当射线OE绕点O逆时针旋转到OF1时，

＝120°－30°＝90°，

当射线OE绕点O逆时针旋转到OF2时，

＝360°－120°－30°＝210°，

故答案为：