题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.
上.
(1)若![]() ,
,![]() .
.
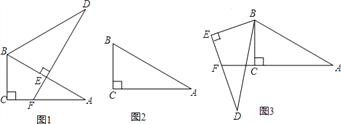
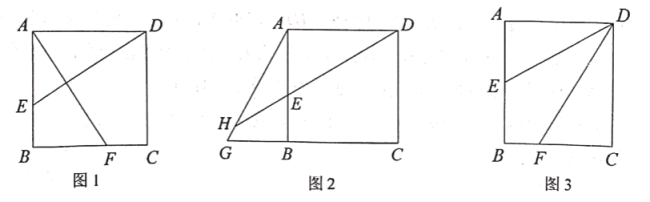
①如图1,求证:![]() ;
;
②如图2,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 的延长线交
的延长线交![]() 于
于![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(2)如图3,若![]() 为
为![]() 的中点,
的中点,![]() .则
.则![]() 的值为 (结果用含
的值为 (结果用含![]() 的式子表示)
的式子表示)
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①由“ASA”可证△ADE≌△BAF可得AE=BF;
②过点A作AF⊥HD交BC于点F,由等腰三角形的性质和平行线的性质可得∠HAF=∠AFG=∠DAF,可得AG=FG,即可得结论;
(2)过点E作EH⊥DF于H,连接EF,由角平分线的性质可得AE=EH=BE,由“HL”可证Rt△BEF≌Rt△HEF,可得BF=FH,由勾股定理可求解.
证明(1)①∵四边形ABCD是矩形,AD=AB,
∴四边形ABCD是正方形,
∴AD=AB,∠DAB=90°=∠ABC,
∴∠DAF+∠BAF=90°,
∵AF⊥DE,
∴∠DAF+∠ADE=90°,
∴∠ADE=∠BAF,且AD=AB,∠DAE=∠ABF=90°,
∴△ADE≌△BAF(ASA),
∴AE=BF;
②如图,过点A作AF⊥HD交BC于点F,
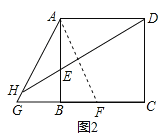
由(1)可知AE=BF,
∵AH=AD,AF⊥HD,
∴∠HAF=∠DAF.
∵AD∥BC,
∴∠DAF=∠AFG,
∴∠HAF=∠AFG,
∴AG=GF,
∴AG=GB+BF=GB+AE;
(3)如图,过点E作EH⊥DF于H,连接EF,
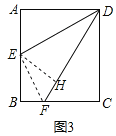
∵E为AB的中点,
∴AE=BE=![]() AB,
AB,
∵∠ADE=∠EDF,EA⊥AD,EH⊥DF,
∴AE=EH,AD=DH=nAB,
∴BE=EH,EF=EF,
∴Rt△BEF≌Rt△HEF(HL),
∴BF=FH,
设BF=x=FH,则FC=BC-BF=nAB-x,
∵DF2=FC2+CD2,
∴(nAB+x)2=(nAB-x)2+AB2,
∴x=![]() =BF,
=BF,
∴FC=![]() AB,
AB,
∴![]() =4n2-1.
=4n2-1.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案