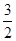题目内容
如图,抛物线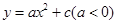 交
交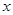 轴于点
轴于点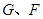 ,交
,交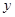 轴于点
轴于点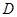 ,在
,在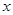 轴上方的抛物线上有两点
轴上方的抛物线上有两点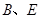 ,它们关于
,它们关于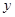 轴对称,点
轴对称,点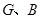 在
在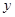 轴左侧.
轴左侧.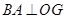 于点
于点 ,
,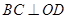 于点
于点 ,四边形
,四边形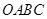 与四边形
与四边形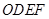 的面积分别为6和10,则
的面积分别为6和10,则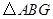 与
与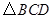 的面积之和为 .
的面积之和为 .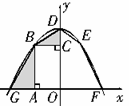
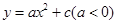 交
交 轴于点
轴于点 ,交
,交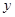 轴于点
轴于点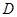 ,在
,在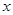 轴上方的抛物线上有两点
轴上方的抛物线上有两点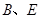 ,它们关于
,它们关于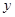 轴对称,点
轴对称,点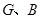 在
在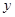 轴左侧.
轴左侧.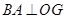 于点
于点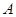 ,
,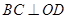 于点
于点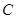 ,四边形
,四边形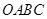 与四边形
与四边形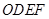 的面积分别为6和10,则
的面积分别为6和10,则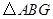 与
与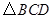 的面积之和为 .
的面积之和为 .
4
试题分析:根据抛物线的对称性知:四边形ODBG的面积应该等于四边形ODEF的面积;由图知△ABG和△BCD的面积和是四边形ODBG与矩形OCBA的面积差,由此得解.
由于抛物线的对称轴是y轴,根据抛物线的对称性知:S四边形ODEF=S四边形ODBG=10;
∴S△ABG+S△BCD=S四边形ODBG-S四边形OABC=10-6=4.
点评:能够根据抛物线的对称性判断出四边形ODEF、四边形ODBG的面积关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,当0<x<3时,y的范围为( ).
,当0<x<3时,y的范围为( ).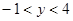

 ≤
≤ ≤
≤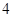
 ≤
≤
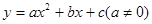 的图象如图所示,
的图象如图所示,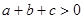 ②
②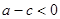 ③
③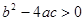 ④
④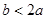 ⑤
⑤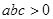
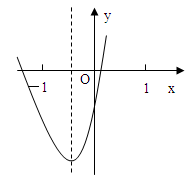
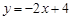 交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线
交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线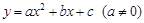 经过点A、B、C.
经过点A、B、C.
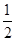 时,求点P的坐标;
时,求点P的坐标;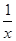 -2实数根的情况是
-2实数根的情况是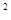 +2的顶点的坐标是( )
+2的顶点的坐标是( )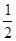 ,2)
,2) x2+x+
x2+x+