题目内容
15. 如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.
如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.
分析 由于C、D是弧AB的三等分点,易得∠AOC=∠DOB,又OA=OB=OC,易证得△AOC≌△OCD,可得∠ACO=∠OCD,易知∠AEC=∠OCD,因此∠ACO=∠AEC,即AE=BF=CD.
解答 解:连接AC、BD,如图所示: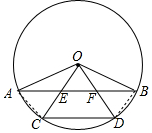
∵C,D是$\widehat{AB}$的三等分点,
∴AC=CD=BD,∠AOC=∠COD,OA=OC=OD,
在△ACO与△DCO中,$\left\{\begin{array}{l}{OA=OD}&{\;}\\{∠AOC=∠DOC}&{\;}\\{OC=OC}&{\;}\end{array}\right.$,
∵∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC,
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD,
∴AE=CD=BF.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3.同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两个立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线y=-x2+3x上的概率为( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
 在数轴上表示下列各数,并把它们按照从小到大的顺序排列
在数轴上表示下列各数,并把它们按照从小到大的顺序排列  如图,在平面直角坐标系中,经过点P(0,2)的直线y=kx+b与二次函数y=$\frac{1}{4}$x2+1的图象相交于A、B两点(点A在点B的左侧).
如图,在平面直角坐标系中,经过点P(0,2)的直线y=kx+b与二次函数y=$\frac{1}{4}$x2+1的图象相交于A、B两点(点A在点B的左侧).