题目内容
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
【答案】(1)3(2)![]()
【解析】解:(1)设乙盒中红球的个数为x,
根据题意得![]() ,解得x=3。
,解得x=3。
经检验,x=3是方程的根。
∴乙盒中红球的个数为3。
(2)列表如下:
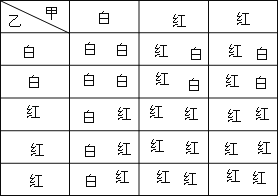
∵共有15种等可能的结果,两次摸到不同颜色的球有7种,
∴两次摸到不同颜色的球的概率=![]() 。
。
(1)设乙盒中红球的个数为x,根据概率公式由从乙盒中随机摸出一个球,摸到红球的概率为![]() 可得到方程得
可得到方程得![]() ,然后解方程即可。
,然后解方程即可。
(2)列表或画树状图展示所有15种等可能的结果数,再找出两次摸到不同颜色的球占7种,然后根据概率公式即可得到两次摸到不同颜色的球的概率。

练习册系列答案
相关题目
【题目】某校为灾区开展了"献出我们的爱"赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎,表中数据有两处被墨水污染,已无法看清,但已知全班平均每人捐款38元
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校1200人中捐款在40元以上(包括40元)的人数是多少?