题目内容
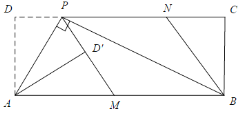
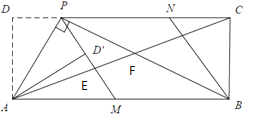
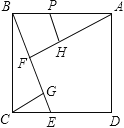
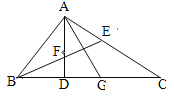
【题目】如图,菱形纸片![]() 的边长为
的边长为![]() 翻折
翻折![]() 使点
使点![]() 两点重合在对角线
两点重合在对角线![]() 上一点
上一点![]() 分别是折痕.设
分别是折痕.设![]() .
.
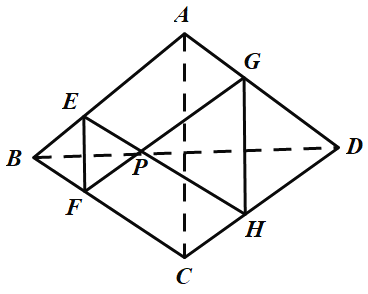
(1)证明:![]() ;
;
(2)当![]() 时,六边形
时,六边形![]() 周长的值是否会发生改变,请说明理由;
周长的值是否会发生改变,请说明理由;
(3)当![]() 时,六边形
时,六边形![]() 的面积可能等于
的面积可能等于![]() 吗?如果能,求此时
吗?如果能,求此时![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
【答案】(1)见解析;(2)不变,见解析;(3)能,![]() 或
或![]()
【解析】
(1)由折叠的性质得到BE=EP,BF=PF,得到BE=BF,根据菱形的性质得到AB∥CD∥FG,BC∥EH∥AD,于是得到结论;
(2)由菱形的性质得到BE=BF,AE=FC,推出△ABC是等边三角形,求得∠B=∠D=60°,得到∠B=∠D=60°,于是得到结论;
(3)记AC与BD交于点O,得到∠ABD=30°,解直角三角形得到AO=1,BO=![]() ,求得S四边形ABCD=2
,求得S四边形ABCD=2![]() ,当六边形AEFCHG的面积等于
,当六边形AEFCHG的面积等于![]() 时,得到S△BEF+S△DGH=
时,得到S△BEF+S△DGH=![]() ,设GH与BD交于点M,求得GM=
,设GH与BD交于点M,求得GM=![]() x,根据三角形的面积列方程即可得到结论.
x,根据三角形的面积列方程即可得到结论.
解:![]() 折叠后
折叠后![]() 落在
落在![]() 上,
上,
![]()
![]()
![]() 平分
平分![]()
![]() ,
,
![]() 四边形
四边形![]() 为菱形,同理四边形
为菱形,同理四边形![]() 为菱形,
为菱形,
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() .
.
![]() 不变.
不变.
理由如下:由![]() 得
得![]()
![]() 四边形
四边形![]() 为菱形,
为菱形,
![]()
![]() 为等边三角
为等边三角
![]() ,
,
![]()
![]() 为定值.
为定值.
![]() 记
记![]() 与
与![]() 交于点
交于点![]() .
.

![]()
![]()
![]()
![]()
![]()
![]()
当六边形![]() 的面积为
的面积为![]() 时,
时,
![]()
由![]() 得
得![]()
![]()
![]()
![]()
记![]() 与
与![]() 交于点
交于点![]()

![]() ,
,![]()
![]()
同理![]()
即![]()
化简得![]()
解得![]() ,
,![]()
∴当![]() 或
或![]() 时,六边形
时,六边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目