Question

【题目】如图，在△ABC中，∠C=90°，AB=5，BC=4，点P在边AB上，若△APC为以AC为腰的等腰三角形，则tan∠BCP=________．

Answer 1

【答案】或

【解析】根据勾股定理求出AC，分AC=AP和CA=CP两种情况，根据相似三角形的性质定理得到比例式，进行计算，根据正切的定义解答即可．

∵∠C=90°，AB=5，BC=4，

∴AC==3．

如图1，当AC=AP时，作PD⊥BC于D，则BP=AB-AP=2，

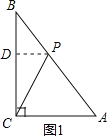
∵∠C=90°，PD⊥BC，

∴PD∥AC，

∴，

∴，

解得，BD=1.6，PD=1.2，

则CD=4-1.6=2.4，

tan∠BCP=；

如图2，当CP=CA时，作CE⊥AB于E，PD⊥BC于D，

∵∠C=90°，CE⊥AB，

∴AC2=AEAB，

解得，AE=1.8，

∵CP=CA，

∴PE=AE=1.8，

则BP=1.4，

PD∥AC，

∴，

∴，

解得，BD=，PD=，

则CD=4-=，

tan∠BCP=，

故答案为：或．