ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÎÊÌâÌáłöŁș
![]() ŁŹ
ŁŹ![]() ·Ö±đÊÇÊČĂŽÊęʱŁŹ¶àÏîÊœ
·Ö±đÊÇÊČĂŽÊęʱŁŹ¶àÏîÊœ![]() șÍ
șÍ![]() șă”ÈŁż
șă”ÈŁż
ÔĶÁÀíœâŁș
ËùÎœșă”ÈÊœŁŹŸÍÊÇ֞ȻÂÛÓĂÈÎșÎÊęÖ”ÀŽŽúÌæÊœÖДıäÁżŁŹŚóĄąÓÒÁœ±ß”ÄÖ”¶ŒÏà”ȔĔÈÊœŁźÎÒĂÇÓĂ·ûșĆĄ°![]() Ą±ÀŽ±íÊŸșă”ÈŁŹ¶ÁŚśĄ°șă”ÈÓÚĄ±ŁźÓÚÊÇŁŹÉÏĂæ”ÄÎÊÌâÒČżÉÒÔ±íÊöÎȘŁșÒŃÖȘ
Ą±ÀŽ±íÊŸșă”ÈŁŹ¶ÁŚśĄ°șă”ÈÓÚĄ±ŁźÓÚÊÇŁŹÉÏĂæ”ÄÎÊÌâÒČżÉÒÔ±íÊöÎȘŁșÒŃÖȘ![]() ŁŹÇóŽę¶šÏ”Êę
ŁŹÇóŽę¶šÏ”Êę![]() ŁŹ
ŁŹ![]() Łź
Łź
ÎÊÌâœâŸöŁș
Łš·œ·š1ĄȘÊęÖ”ŽúÈë·šŁ©ÓÉșă”ÈÊœ”ÄžĆÄÎÒĂÇĂżÓĂÒ»žöÊęÖ”ÀŽŽúÌæÎÊÌâÖĐ”Ä![]() ŁŹŒŽżÉ”Ă”œÒ»žöčŰÓÚ
ŁŹŒŽżÉ”Ă”œÒ»žöčŰÓÚ![]() Óë
Óë![]() ”Ä·œłÌŁźÒòŽËŁŹÒȘÇółö
”Ä·œłÌŁźÒòŽËŁŹÒȘÇółö![]() Óë
Óë![]() ”ÄÖ”ŁŹÖ»ĐèÒȘÓĂÁœžöȻ͏”ÄÊęÖ”·Ö±đŽúÌæÊœÖĐ”Ä
”ÄÖ”ŁŹÖ»ĐèÒȘÓĂÁœžöȻ͏”ÄÊęÖ”·Ö±đŽúÌæÊœÖĐ”Ä![]() ŁŹŸÍżÉÒԔԜһžöčŰÓÚ
ŁŹŸÍżÉÒԔԜһžöčŰÓÚ![]() Óë
Óë![]() ”ĶțÔȘÒ»ŽÎ·œłÌŚéŁŹœâŐâžö·œłÌŚéŁŹŒŽżÉÇó”Ă
”ĶțÔȘÒ»ŽÎ·œłÌŚéŁŹœâŐâžö·œłÌŚéŁŹŒŽżÉÇó”Ă![]() Óë
Óë![]() Łź
Łź
œâŁș·Ö±đÓĂ![]() ŁŹ
ŁŹ![]() ŽúÌæÊœÖĐ”Ä
ŽúÌæÊœÖĐ”Ä![]() ŁŹ”Ă
ŁŹ”Ă
![]()
œâÖźŁŹ”Ă![]()
Łš·œ·š2ĄȘÏ”Êę±ÈœÏ·šŁ©
¶šÀí Èçčû![]() ŁŹ
ŁŹ
ÄÇĂŽ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() Łź
Łź
žùŸĘŐâžö¶šÀíŁŹÒČżÉÒÔŐâŃùœâŁș
œâŁșÓÉÌâÉè![]() ŁŹ
ŁŹ
±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏”Ă![]() ŁŹ
ŁŹ![]() Łź
Łź
Çë»ŰŽđÏÂĂæ”ÄÎÊÌâŁș
Łš1Ł©ÒŃÖȘ¶àÏîÊœ![]() ŁźÇó
ŁźÇó![]() Óë
Óë![]() ”ÄÖ”Ł»
”ÄÖ”Ł»
Łš2Ł©Èçčû![]() ±»
±»![]() łęșóÓà
łęșóÓà![]() ŁŹÇó
ŁŹÇó![]() ”ÄÖ”Œ°ÉÌÊœŁź
”ÄÖ”Œ°ÉÌÊœŁź
ĄŸŽđ°žĄżŁš1Ł©m=-1ŁŹn=2Ł»Łš2Ł©![]() ŁŹÉÌÊœÎȘ
ŁŹÉÌÊœÎȘ![]() Łź
Łź
ĄŸœâÎöĄż
Łš1Ł©¶Ô¶àÏîÊœÓÒ±ßÀûÓöàÏîÊœłË¶àÏîÊœ”Ä·šÔòŐčżȘŁŹ±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏”Ă”œ·œłÌŚéŁŹœâÖźŒŽżÉŁ»
Łš1Ł©ÏÈžùŸĘÌâÒâżÉÖȘÉÌÊœ”ÄÒ»ŽÎÏîÏ”ÊęÎȘ1ŁŹčÊżÉÉèÉÌÊœÎȘ![]() ŁŹÔÙžùŸĘÌâÒ⣏±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏ÁĐłö·œłÌŒŽżÉÇółö
ŁŹÔÙžùŸĘÌâÒ⣏±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏ÁĐłö·œłÌŒŽżÉÇółö![]() Ąą
Ąą![]() ”ÄÖ”Łź
”ÄÖ”Łź
Łš1Ł©![]()
![]() ŁŹ
ŁŹ
±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏”Ă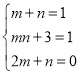 ŁŹ
ŁŹ
œâÖźŁŹ”Ă![]() Ł»
Ł»
Łš2Ł©ÒòÎȘ![]() ŁŹËùÒÔÉÌÊœ”ÄŚîžßŽÎÏîÎȘÒ»ŽÎŁŹČąÇÒÏ”ÊęÎȘ
ŁŹËùÒÔÉÌÊœ”ÄŚîžßŽÎÏîÎȘÒ»ŽÎŁŹČąÇÒÏ”ÊęÎȘ![]() Łź
Łź
ĄàÉèÉÌÊœÎȘ![]() ŁŹÓÉÌâÒ⣏”ĂŁș
ŁŹÓÉÌâÒ⣏”ĂŁș
![]()
![]() ŁŹ
ŁŹ
±ÈœÏ¶ÔÓŠÏî”ÄÏ”Ê꣏”Ă![]() ŁŹ
ŁŹ
œâÖźŁŹ”Ă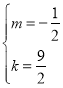
![]() ŁŹÉÌÊœÎȘ
ŁŹÉÌÊœÎȘ![]() Łź
Łź

 Ò»±ŸșĂÌâżÚËăÌâżšÏ”ÁĐŽđ°ž
Ò»±ŸșĂÌâżÚËăÌâżšÏ”ÁĐŽđ°ž