题目内容
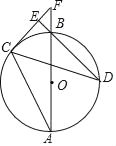
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
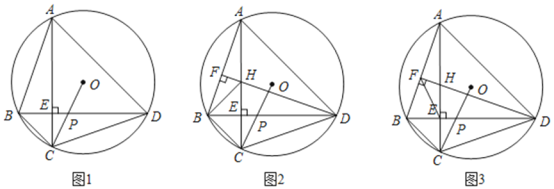
(1)如图1,求证:![]() ;
;
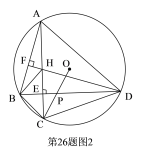
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
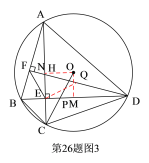
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)延长CO交⊙O于K,连接DK,利用圆周角定理得到∠CDK=90°,根据AC⊥BD及圆周角定理求得∠CBD=∠CKD,即可求出结论;
(2)根据垂直的定义及圆周角定理得到∠BDC=∠BDF,得到DB垂直平分CH,即可证得结论;
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,先证△AED与△BEC都为等腰直角三角形,根据 △AEF≌△DEQ求出![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
,得到AE=ED=12,再利用BE:DE=1:3及勾股定理求出OC即可.
(1)解:延长CO交⊙O于K,连接DK.
∵CK为⊙O直径,
∴∠CDK=90°,
∴∠OCD+∠CKD=90°,
∵AC⊥BD于E ,
∴∠BEC=90°,
∴∠ACB+∠CBD=90°,
∵∠CBD=∠CKD,
∴∠ACB=∠OCD ;

(2)∵DF⊥AB于F,
∴∠DFB=90°,
∵AC⊥BD于E,
∴∠AEB=90°,
∴∠BAC+∠DBF=90°,
∴∠BDF+∠DBF=90°,
∴∠BDF=∠BAC,
∵∠BAC=∠BDC,
∴∠BDC=∠BDF,
∴∠DHC=∠DCH,
∴DB垂直平分CH,
∴BH=BC;
(3)作EQ⊥EF交FD于Q,ON⊥AC于N,OM⊥BD于M ,
∵BC∥AD,
∴∠BCA=∠DAC,
∵∠BCA=∠ADB,
∴∠DAC=∠ADB,
∴△AED与△BEC都为等腰直角三角形,
∵△AEF≌△DEQ,
∴AF=QD=![]() ,EF=EQ=
,EF=EQ=![]() ,
,
∴FQ=![]() ,
,
∴![]() ,勾股定理得AD=
,勾股定理得AD=![]() ,
,
∴AE=ED=12,
∵BE:DE=1:3,
∴BE=CE=4,
∴BD=AC=16,
∴BM=CN=8,
∴OM=EN=4,
∴ON=EM=4,
∴OC=![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案