题目内容
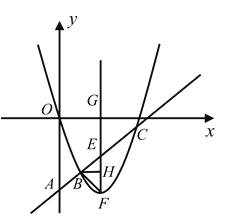
【题目】已知：二次函数y=x2+bx+c经过原点，且当x=2时函数有最小值；直线AC解析式为y=kx-4，且与抛物线相交于B、C．
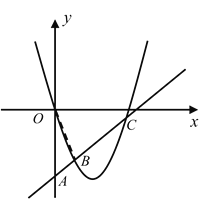
（1）求二次函数解析式；
（2）若S△AOB∶S△BOC=1：3，求直线AC的解析式；
（3）在（2）的条件下，点E为线段BC上一动点（不与B、C重合），过E作x轴的垂线交抛物线于F、交x轴于G，是否存在点E，使△BEF和△CGE相似？若存在，请求出所有点E的坐标；若不存在，请说明理由．
【答案】（1）y=x2-4x；（2）直线AC的解析式为y=x-4；（3）存在，E点坐标为E(3．-1)或E(2，-2 ) ．
【解析】
（1）根据二次函数y=x2+bx+c经过原点可知c=0，当x=2时函数有最小值可知对称轴是x=2，故可求出b，即可求解；
（2）连接OB，OC，过点C作CD⊥y轴于D，过点B作BE⊥y轴于E，根据
得到
，
，由EB∥DC，对应线段成比例得到
，再联立y=kx-4与y=x2-4x得到方程 kx-4=x2-4x，即x2-（k+4）x+4=0，求出x1,x2，根据x1,x2之间的关系得到关于k的方程即可求解；
（3）根据（1）（2）求出A,B,C的坐标，设E（m，m-4）（1＜m＜4）则G（m，0）、F（m，m2-4m），根据题意分∠EFB=90°和∠EBF=90°，分别找到图形特点进行列式求解．
解：（1）∵二次函数y=x2+bx+c经过原点，
∴c=0
∵当x=2时函数有最小值
∴
，
∴b=-4，c=0，
∴y=x2-4x；
（2）如图，连接OB，OC，过点C作CD⊥y轴于D，过点B作BE⊥y轴于E，
∵
∴
∴
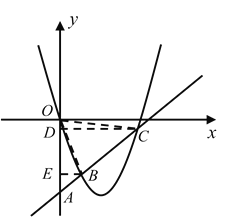
∵EB∥DC
∴
∵y=kx-4交y=x2-4x于B、C
∴kx-4=x2-4x，即x2-（k+4）x+4=0
∴
，或
∵xB＜xC
∴EB=xB=
，DC=xC=
∴4=
解得 k=-9（不符题意，舍去）或k=1
∴k=1
∴直线AC的解析式为y=x-4；
（3）存在．理由如下：
由题意得∠EGC=90°，
∵直线AC的解析式为y=x-4
∴A(0，-4 ) ，C（4，0）
联立两函数得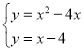
，解得
或
∴B（1，-3）
设E（m，m-4）（1＜m＜4）
则G（m，0）、F（m，m2-4m）
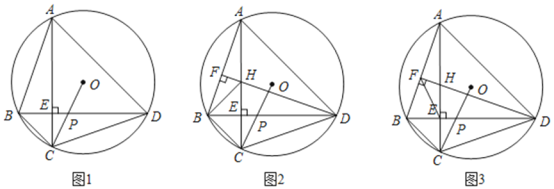
①如图，当∠EFB=90°，即CG//BF时，△BFE∽△CGE．
此时F点纵坐标与B点纵坐标相等．
∴F（m，-3）
即m2-4m=-3
解得m=1（舍去）或m=3
∴F（3，-3）
故此时E（3，-1）
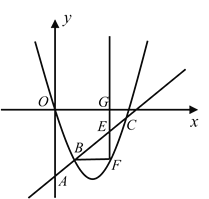
②如图当∠EBF=90°，△FBE∽△CGE
∵C（4，0），A(0 ，4 )
∴OA=OC
∴∠GCE=45°=∠BEF=∠BFE
过B点做BH⊥EF，
则H（m,-3）∴BH=m-1
又∵∠GCE=45°=∠BEF=∠BFE
∴△BEF是等腰直角三角形，又BH⊥EF
∴EH=HF，EF=2BH
∴(m-4)- (m2-4m) =2(m-1)
解得m1=1（舍去）m2=2
∴E(2,-2)
综上，E点坐标为E(3.-1)或E(2,-2)．
