题目内容
【题目】如图，在边长为1的正方形网格中，A的坐标为（0，0），B的坐标为（﹣3，1）．
（1）将线段AB绕点A逆时钟旋转θ度（0＜θ＜180），得到对应的线段AE，当AE∥CD时，设在此过程中线段AB所扫过的区域面积为S，点B所经过的路径长为l，则S＝ ；l＝ ．
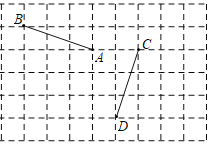
（2）是否存在点P，使得线段AB可由线段CD绕点P旋转一个角度而得到？若存在，直接写出点P的坐标（写出一个即可）；若不存在，请说明理由．
【答案】（1）
；
；（2）存在点P，P（1，1）或（﹣1，﹣2）．
【解析】
（1）先根据要求画出图形，利用扇形的面积公式S=
，弧长公式l＝
计算即可；
（2）根据题意，作出平面直角坐标系，分两种情形：①当A与C对应，B与D对应；②当A与D对应，B与C对应，在两种情况下分别连接两组对应点得出两条线段，再分别作这两条线段的中垂线，两条中垂线相交的点就是旋转中心，从而解决问题．
解：（1）如图，线段AE即为所求．
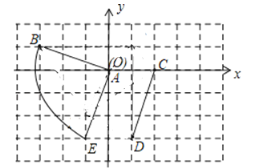
根据图形可知，AB的旋转角为90°，又AB=
，
∴S＝
＝
，l＝
＝
．
故答案为；；
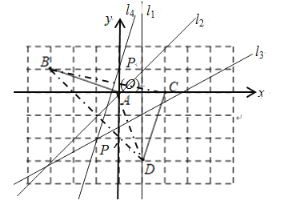
（2）存在点P，
当A与C对应，B与D对应时，分别作出线段AC，BD的中垂线l1，l2，l1与l2的交点即为点P，根据图形可知旋转中心P的坐标为（1，1）；
当A与D对应，B与C对应时，分别作出线段AD，BC的中垂线l3，l4，l3与l4的交点即为点P′，根据图形可知旋转中心P′的坐标为（﹣1，﹣2）．
故点P的坐标为（1，1）或（﹣1，﹣2）．
练习册系列答案
相关题目
