题目内容
在
ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，且AB=6，BC=10，则OE= .
ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，且AB=6，BC=10，则OE= .5.
试题分析：画出图形，根据平行线的性质，结合点E是边CD的中点，可判断OE是△DBC的中位线，从而可得出OE的长度：
∵四边形ABCD是平行四变形，∴点O是BD中点.
∵点E是边CD的中点，∴OE是△DBC的中位线.
∴OE=
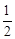BC=5.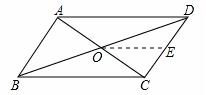
练习册系列答案
考前必练系列答案
相关题目
，那么AC的长等于（ ）
cm2 B．
cm2 C．
cm2 D．
cm2