题目内容
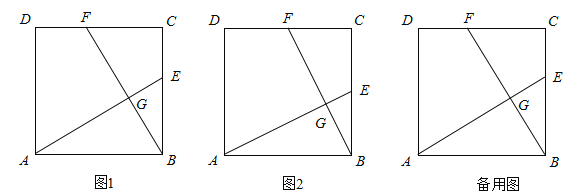
【题目】正方形ABCD的边长为4,点E在BC上,点F在CD上,且CF=BE,AE与BF交于G点.
(1)如图1,求证:①AE=BF,②AE⊥BF.
(2)连接CG并延长交AB于点H,
①若点E为BC的中点(如图2),求BH的长;
②若点E在BC的边上滑动(不与B、C重合),当CG取得最小值时,求BE的长.
【答案】(1)①见解析;②见解析;(2)①BH=![]() ;②2
;②2![]() ﹣2.
﹣2.
【解析】
(1)①由正方形的性质得出AB=BC=4,∠ABC=∠BCD=90°,由SAS证明△ABE≌△BCF,即可得出结论;
②由①得:△ABE≌△BCF,得出∠BAE=∠CBF,证出∠AGB=90°,即可得出结论;
(2)①由直角三角形的性质得出CF=BE=![]() BC=2,由勾股定理得出BF=2
BC=2,由勾股定理得出BF=2![]() ,由(1)得:AE⊥BF,则∠BGE=∠ABE=90°,证明△BEG∽△AEB,得出
,由(1)得:AE⊥BF,则∠BGE=∠ABE=90°,证明△BEG∽△AEB,得出![]() =
=![]() ,设GE=x,则BG=2x,在Rt△BEG中,由勾股定理得出方程,解方程得出BG=2×
,设GE=x,则BG=2x,在Rt△BEG中,由勾股定理得出方程,解方程得出BG=2×![]() ,由平行线得出
,由平行线得出![]() ,即可得出BH的长;
,即可得出BH的长;
②由(1)得:∠AGB=90°,得出点G在以AB为直径的圆上,设AB的中点为M,当C、G、M在同一直线上时,CG为最小值,求出GM=![]() AB=BM=2,由平行线得出
AB=BM=2,由平行线得出![]() =1,证出CF=CG=BE,设CF=CG=BE=a,则CM=a+2,在Rt△BCM中,由勾股定理得出方程,解方程即可.
=1,证出CF=CG=BE,设CF=CG=BE=a,则CM=a+2,在Rt△BCM中,由勾股定理得出方程,解方程即可.
(1)证明:①∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=∠BCD=90°,
在△ABE和△BCF中,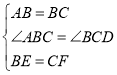 ,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
②由①得:△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AGB=90°,
∴AE⊥BF;
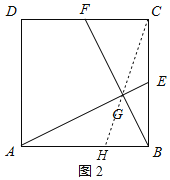
(2)解:①如图2所示:
∵E为BC的中点,
∴CF=BE=![]() BC=2,
BC=2,
∴BF![]() ,
,
由(1)得:AE⊥BF,
∴∠BGE=∠ABE=90°,
∵∠BEG=∠AEB,
∴△BEG∽△AEB,
∴![]() ,
,
设GE=x,则BG=2x,
在Rt△BEG中,由勾股定理得:x2+(2x)2=22,
解得:x=![]() ,
,
∴BG=2×![]() ,
,
∵AB∥CD,
∴![]() ,即
,即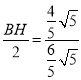 ,
,
解得:BH=![]() ;
;
②由(1)得:∠AGB=90°,
∴点G在以AB为直径的圆上,
设AB的中点为M,
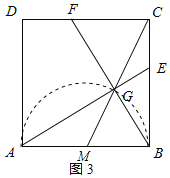
由图形可知:当C、G、M在同一直线上时,CG为最小值,如图3所示:
∵AE⊥BF,
∴∠AGB=90°,
∴GM=![]() AB=BM=2,
AB=BM=2,
∵AB∥CD,
∴![]() =1,
=1,
∴CF=CG,
∵CF=BE,
∴CF=CG=BE,
设CF=CG=BE=a,则CM=a+2,
在Rt△BCM中,由勾股定理得:22+42=(a+2)2,
解得:a=2![]() ﹣2,即
﹣2,即
当CG取得最小值时,BE的长为2![]() ﹣2.
﹣2.

 名校课堂系列答案
名校课堂系列答案