题目内容
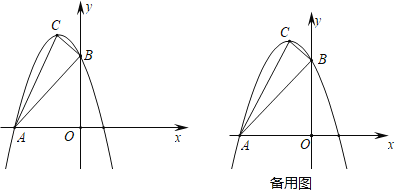
【题目】在平面直角坐标系XOY中,抛物线y=﹣x2+bx+c经过点A(﹣2,0),B(8,0).
(1)求抛物线的解析式;
(2)点C是抛物线与y轴的交点,连接BC,设点P是抛物线上在第一象限内的点,PD⊥BC,垂足为点D.
①是否存在点P,使线段PD的长度最大?若存在,请求出点P的坐标;若不存在,请说明理由;
②当△PDC与△COA相似时,直接写出点P的坐标.
【答案】(1)![]() ;(2)①当P(4,6)时,PD的长度最大,最大值是
;(2)①当P(4,6)时,PD的长度最大,最大值是![]() ;②当△PDC与△COA相似时,点P的坐标为(6,4)或(3,
;②当△PDC与△COA相似时,点P的坐标为(6,4)或(3,![]() ).
).
【解析】
(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,即可求解;
(2)①在Rt△PDE中,PD=PEsin∠PED=PEsin∠OCB=![]() PE,即可求解;②分∠PCD=∠CBO、∠PCD=∠BCO两种情况,分别求解.
PE,即可求解;②分∠PCD=∠CBO、∠PCD=∠BCO两种情况,分别求解.
(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)由(1)知C(0,4),∵B(8,0),
将点B、C的坐标代入一次函数表达式并解得:
直线BC的解析式为:y=﹣![]() x+4,
x+4,
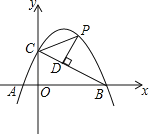
①如图1,过P作PG⊥x轴于G,PG交BC于E,
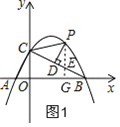
Rt△BOC中,OC=4,OB=8,
∴BC=![]() ,
,
在Rt△PDE中,PD=PEsin∠PED=PEsin∠OCB=![]() PE,
PE,
∴当线段PE最长时,PD的长最大,
设P(t,![]() ),则E(t,﹣
),则E(t,﹣![]() t+4),
t+4),
∴PE=PG﹣EG=![]() ,(0<t<8),
,(0<t<8),
当t=4时,PE有最大值是4,此时P(4,6),
∴PD═![]() ,
,
即当P(4,6)时,PD的长度最大,最大值是![]() ;
;
②∵A(﹣2,0),B(8,0),C(0,4),
∴OA=2,OB=8,OC=4,
∴AC2=22+42=20,AB2=(2+8)2=100,BC2=42+82=80,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△COA∽△BOC,
当△PDC与△COA相似时,就有△PDC与△BOC相似,
∵相似三角形的对应角相等,
∴∠PCD=∠CBO或∠PCD=∠BCO,
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
此时CP∥OB,
∵C(0,4),
∴yP=4,
∴![]() =4,
=4,
解得:x1=6,x2=0(舍),
即Rt△PDC∽Rt△COB时,P(6,4);
(II)若∠PCD=∠BCO时,
即Rt△PDC∽Rt△BOC,
如图2,过P作x轴的垂线PG,交直线BC于F,
∴PF∥OC,
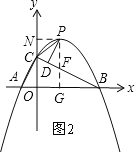
∴∠PFC=∠BCO,
∴∠PCD=∠PFC,
∴PC=PF,
设P(n,![]() ),则PF=﹣
),则PF=﹣![]() n2+2n,
n2+2n,
过P作PN⊥y轴于N,
Rt△PNC中,PC2=PN2+CN2=PF2,
∴n2+(![]() ﹣4)2=(﹣
﹣4)2=(﹣![]() n2+2n)2,
n2+2n)2,
解得:n=3,
即Rt△PDC∽Rt△BOC时,P(3,![]() );
);
综上所述,当△PDC与△COA相似时,点P的坐标为(6,4)或(3,![]() ).
).