题目内容
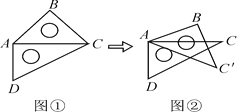
【题目】取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′,如图②所示.设∠CAC′=α(0°<α≤45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化,若变化 ,求出变化范围;若不变,求出其度数.
【答案】(1)见解析;(2)∠DBC′+∠CAC′+∠BDC的度数不变,105°.
【解析】
(1)根据三角板的特殊角度值即可求解.
(2)作出辅助线,根据三角形内角和即可解题.
(1)证明:∵∠CAC′=15°,
∴∠BAC=∠BAC′-∠CAC′=45°-15°=30°,
又∴∠C=30°,
∴∠BAC=∠C,
∴AB∥CD;
(2)解:∠DBC′+∠CAC′+∠BDC的度数不变.
如图,连接CC′.
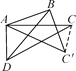
∵∠DBC′+∠BDC=∠DCC′+∠BC′C,
∠CAC′+∠ACC′+∠AC′C=180°,
∴∠CAC′+∠AC′B+∠BC′C+∠ACD+∠DCC′=180°,
∵∠AC′B=45°,∠ACD=30°,
∴∠DBC′+∠CAC′+∠BDC=180°-45°-30°=105°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?