题目内容
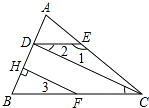
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
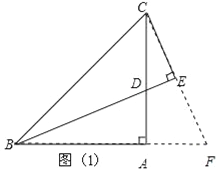
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
【答案】(1)①22.5°②BD=2CE(2)BE﹣CE=2AF
【解析】试题分析:(1)①根据等腰直角三角形的性质得出∠CBA=45°,再利用角平分线的定义解答即可;②延长CE交BA的延长线于点F得出CE=FE,再利用AAS证明△ABD≌△ACF,利用全等三角形的性质解答即可;(2)过点A作AH⊥AE,交BE于点H,证明△ABH≌△ACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
试题解析:
(1)①∵在△ABC中,∠BAC=90°,AB=AC,
∴∠CBA=45°,∵BD平分∠ABC,∴∠DBA=22.5°,
∵CE⊥BD,∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,∴∠ECD=∠DBA=22.5°;
②BD=2CE.
证明:延长CE交BA的延长线于点F,如图1,
∵BD平分∠ABC,CE⊥BD,
∴CE=FE,
在△ABD与△ACF中,
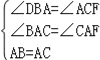 ,
,
∴△ABD≌△ACF(AAS),
∴BD=CF=2CE;
(2)结论:BE﹣CE=2AF.
证明:过点A作AH⊥AE,交BE于点H,如图2,

∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH与△ACE中,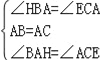 ,
,
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH是等腰直角三角形,
∴AF=EF=HF,
∴BE﹣CE=2AF.

 阅读快车系列答案
阅读快车系列答案