题目内容
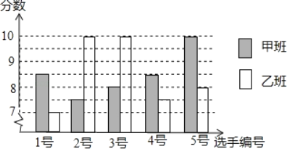
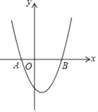
【题目】对于某一函数给出如下定义：若存在实数m，自变量的值为m 时，函数值等于m，则称m为这个函数的反向值.在函数存在反向值时，该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地，当函数只有一个反向值时，其反向距离n为零. 例如：图中的函数有 4，－1两个反向值，其反向距离 n 等于 5. 现有函数y＝
，则这个函数的反向距离的所有可能值有（ ）
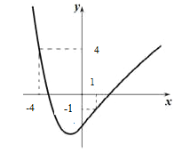
A. 1个B. 2个C. 3个及以上的有限个D. 无数个
【答案】B
【解析】
根据题目中的函数解析式和题目中的新定义，写出这个函数的反向距离的所有可能值，并写出相应m的取值范围． ．
解：∵y＝
∴当x≥k时，
-k=k2-3k，得k=0或k=2，
∴n=2-0=2，
∴k＞2或k≤-2；
当x＜k时，
-k=-k2-3k，
解得，k=0或k=-4，
∴n=0-（-4）=4，
∴-2＜k≤2，
由上可得，当k＞2或k≤-2时，n=2，
当-2＜k≤2时，n=4．
∴这个函数的反向距离的所有可能值有两个.
故选：B.
备战中考寒假系列答案
【题目】我市某公司分两次采购了一批原料，已知第二次的采购数量是第一次采购数量的两倍，其它信息如下表：
第一次 | 第二次 | |
每吨原料的价格（元） | m+500 | m-500 |
采购费用（万元） | 40 | 60 |
（1）求m的值，并求出这两次共采购了多少吨原料？
（2）该公司可将原料加工成A型产品或B型产品，而受设备限制每天只能安排加工一种型号产品．经统计，加工A型产品与B型产品各1天共需用原料数为20吨，加工3天A型产品与加工2天B型产品所需用原料数相等．请求出加工成A，B型产品每天所需的原料数分别是多少吨？
（3）该公司将生产的两种产品全部出口国外，每吨原料加工成A，B型产品后的获利分别是1000元与600元，但要求加工时间不超过30天．为了使总利润获得最大，应采用怎样的加工方案？
【题目】中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：
（1）根据如图填写如表：
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
（2）根据如表数据，分析哪个班的成绩较好，请详细说明．
