题目内容
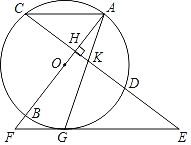
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
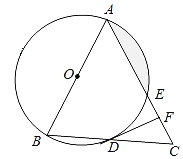
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CFAC;
(3)若⊙O的半径为2![]() ,∠CDF=15°,求阴影部分的面积.
,∠CDF=15°,求阴影部分的面积.
【答案】(1)见解析;(2)见解析;(3)4π﹣3![]()
【解析】
(1)如图所示,连接OD,证明∠CDF+∠ODB=90°,即可求解;
(2)证明△CFD∽△CDA,则CD2=CFAC,即BC2=4CFAC;
(3)S阴影部分=S扇形OAE﹣S△OAE即可求解.
解:(1)如图所示,连接OD,
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ODB=∠ABC=∠C,
∵DF⊥AC,
∴∠CDF+∠C=90°,
∴∠CDF+∠ODB=90°,
∴∠ODF=90°,
∴直线DF是⊙O的切线;
(2)连接AD,则AD⊥BC,则AB=AC,
则DB=DC=![]() BC,
BC,
∵∠CDF+∠C=90°,∠C+∠DAC=90°,
∴∠CDF=∠DAC,
∵∠DFC=∠ADC=90°,
∴△CFD∽△CDA,
∴CD2=CFAC,即BC2=4CFAC;
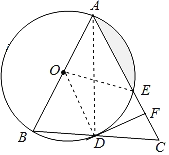
(3)连接OE,
∵∠CDF=15°,∠C=75°,
∴∠OAE=30°=∠OEA,
∴∠AOE=120°,
S△OAE=![]() AE×OEsin∠OEA=
AE×OEsin∠OEA=![]() ×2×2
×2×2![]() ×cos30°×2
×cos30°×2![]() ×sin30°=3
×sin30°=3![]() ,
,
S阴影部分=S扇形OAE﹣S△OAE=![]() ×π×(2
×π×(2![]() )2﹣3
)2﹣3![]() =4π﹣3
=4π﹣3![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.