题目内容
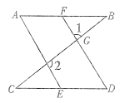
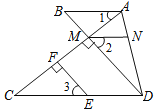
【题目】如图，已知：EF⊥AC，垂足为点F，DM⊥AC，垂足为点M，DM的延长线交AB于点B，且∠1＝∠C，点N在AD上，且∠2＝∠3，试说明AB∥MN.
【答案】证明见解析.
【解析】试题分析：因为EF⊥AC，DM⊥AC得到EF∥DM，根据平行线的性质得∠3＝∠CDM，则∠2＝∠CDM，根据平行线的判定得到MN∥CD，所以∠AMN＝∠C，又∠1＝∠C，于是∠1＝∠AMN，然后根据平行线的判定得到AB∥MN.
试题解析：
∵EF⊥AC，DM⊥AC，
∴∠CFE＝∠CMD＝90°（垂直定义），
∴EF∥DM（同位角相等，两直线平行），
∴∠3＝∠CDM（两直线平行，同位角相等）
∵∠3＝∠2（已知）
∴∠2＝∠CDM（等量代换）
∴MN∥CD（内错角相等，两直线平行）
∴∠AMN＝∠C（两直线平行，同位角相等）
∵∠1＝∠C（已知）
∴∠1＝∠AMN（等量代换）
∴AB∥MN（内错角相等，两直线平行）
练习册系列答案
阅读快车系列答案
相关题目
