题目内容
【题目】等腰三角形一腰上的高与另一腰的夹角为38°,则该等腰三角形的底角的度数为__________
【答案】64°或26°
【解析】
等腰三角形分锐角和钝角两种情况,求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数.
①若∠A<90°,如图1所示:

∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=38°,
∴∠A=90°38°=52°,
∵AB=AC,
∴∠ABC=∠C=![]() (180°52°)=64°;
(180°52°)=64°;
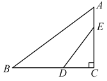
②若∠A>90°,如图2所示:

同①可得:∠DAB=90°38°=52°,
∴∠BAC=180°52°=128°,
∵AB=AC,
∴∠ABC=∠C=![]() (180°128°)=26°;
(180°128°)=26°;
综上所述:等腰三角形底角的度数为64°或26°.
故答案为64°或26°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目