题目内容
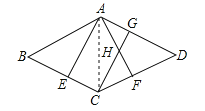
【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

【答案】(1)![]() ;(2)120°
;(2)120°
【解析】试题分析:(1)连接AC,根据线段垂直平分线上的点到两端点的距离相等可得AB=AC,然后判断出△ABC是等边三角形,再根据等边三角形的性质求出AE,然后利用菱形的面积公式列式计算即可得解;
(2)根据等边三角形的性质求出∠CAE,再求出∠CAF,从而得到∠EAF,然后根据两直线平行,同旁内角互补求出∠CHA的度数.
试题解析:解:(1)如图,连接AC.∵E为BC的中点,AE⊥BC,∴AB=AC.又∵菱形的边AB=BC,∴△ABC是等边三角形,∴AE=![]() AB=
AB=![]() ×4=2
×4=2![]() ,∴菱形ABCD的面积=BCAE=4×2
,∴菱形ABCD的面积=BCAE=4×2![]() =8
=8![]() ;
;
(2)在等边三角形ABC中,∵AE⊥BC,∴∠CAE=![]() ∠BAC=
∠BAC=![]() ×60°=30°,同理∠CAF=30°,∴∠EAF=∠CAE+∠CAF=30°+30°=60°.∵AE∥CG,∴∠CHA=180°﹣∠EAF=180°﹣60°=120°.
×60°=30°,同理∠CAF=30°,∴∠EAF=∠CAE+∠CAF=30°+30°=60°.∵AE∥CG,∴∠CHA=180°﹣∠EAF=180°﹣60°=120°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.