题目内容
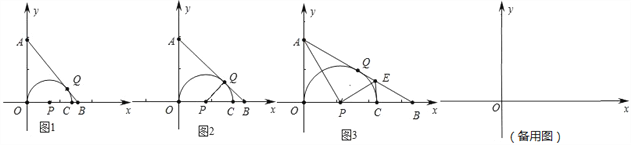
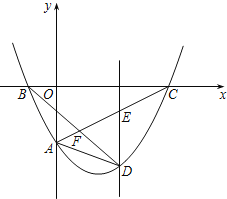
【题目】如图,经过点A(0,﹣2)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,D为第四象限内抛物线上一点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,D为第四象限内抛物线上一点.
(1)求抛物线的解析式;
(2)过点D作y轴的平行线交AC于点E,若AD=AE,求点D的坐标;
(3)连接BD交AC于点F,求![]() 的最大值.
的最大值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)(2,﹣3);(3)
x﹣2;(2)(2,﹣3);(3)![]() .
.
【解析】试题分析:
(1)把点A、B的坐标代入y=![]() x2+bx+c中列方程组解得b、c的值即可得到二次函数的解析式;
x2+bx+c中列方程组解得b、c的值即可得到二次函数的解析式;
(2)如图1,过点A作AH⊥DE于点H,由(1)中所得二次函数的解析式可求得点C的坐标,再由A、C坐标可求得直线AC的解析式,设出点D的坐标,则可表达出点E的坐标,由已知条件易得EH=DH,从而可列出方程求得点D的坐标;
(3)如图2,过点D作DG⊥AC于点G,连接AB,先由已知条件易证△DGE∽△COA,结合(2)可得:DG=![]() DE=
DE=![]() (﹣
(﹣![]() m2+2m)=﹣
m2+2m)=﹣![]() (m2﹣4m);再利用勾股定理逆定理证∠BAC=90°,从而可证△DGF∽△BAF,由此可得:
(m2﹣4m);再利用勾股定理逆定理证∠BAC=90°,从而可证△DGF∽△BAF,由此可得: ![]() =﹣
=﹣![]() (m2﹣4m)=﹣
(m2﹣4m)=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,即可得到:
,即可得到: ![]() 的最大值.
的最大值.
试题解析:
(1)∵点A(0,﹣2)和点B(﹣1,0)均在抛物线上,
∴有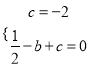 ,解得
,解得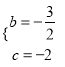 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)过点A作AH⊥DE,垂足为H,如图1.
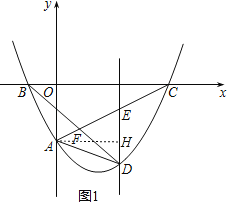
在y=![]() x2﹣
x2﹣![]() x﹣2中,令y=0得,x=﹣1或x=4,
x﹣2中,令y=0得,x=﹣1或x=4,
∴点C坐标为(4,0).
∵点A坐标为(0,﹣2),
∴直线AC的解析式为y=![]() x﹣2.
x﹣2.
设点D坐标为(m, ![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
则点E坐标为(m, ![]() m﹣2),点H坐标为(m,﹣2).
m﹣2),点H坐标为(m,﹣2).
∵AD=AE,AH⊥DE,
∴DH=HE,即﹣2﹣(![]() m2﹣
m2﹣![]() m﹣2)=
m﹣2)=![]() m﹣2﹣(﹣2),
m﹣2﹣(﹣2),
解得m1=2,m2=0(不合题意,舍去).
此时, ![]() m2﹣
m2﹣![]() m﹣2=﹣3,
m﹣2=﹣3,
∴点D的坐标为(2,﹣3).
(3)过点D作DG⊥AC,垂足为G,连接AB,DE交x轴于点P,如图2.
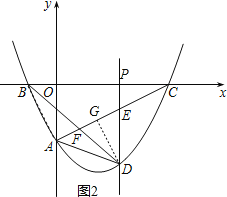
由(2)得,DE=﹣![]() m2+2m.
m2+2m.
∵点A(0,﹣2),点B(﹣1,0),点O(0,0),点C(4,0),
∴AB=![]() ,AC=2
,AC=2![]() ,BC=5,OC=4,OA=2.
,BC=5,OC=4,OA=2.
∵DE∥y轴,DG⊥AC,
∴∠DGE=∠CPE=90°,
∵∠DEG=∠CEP(对顶角),
∴∠EDG=∠ECP=∠ACO.
又∵∠DGE=∠COA=90°,
∴△DGE∽△COA,
∴![]() ,
,
∴DG=![]() DE=
DE=![]() (﹣
(﹣![]() m2+2m)=﹣
m2+2m)=﹣![]() (m2﹣4m).
(m2﹣4m).
∵AB=![]() ,AC=2
,AC=2![]() ,BC=5,
,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
又∵∠DFG=∠BFA,
∴△DGF∽△BAF.
∴![]() =﹣
=﹣![]() (m2﹣4m)=﹣
(m2﹣4m)=﹣![]() (m﹣2)2+
(m﹣2)2+![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由