题目内容
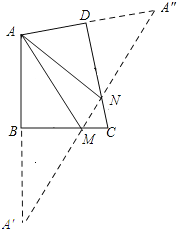
【题目】如图，AB⊥BC，AD⊥DC，∠BAD=100°，在BC、CD上分别找一点M、N，当△AMN的周长最小时，∠AMN+∠ANM的度数是_____．
【答案】160°．
【解析】根据要使△AMN的周长最小，即利用点的对称，使三角形的三边在同一直线上，作出A关于BC和CD的对称点A′，A″，即可得出∠AA′M+∠A″=∠AA″A′=80°，进而得出∠AMN+∠ANM=2（∠AA′M+∠A″），即可得出答案．
作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值．
∵∠DAB=100°，
∴∠AA′M+∠A″=80°．
由轴对称图形的性质可知：∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×80°=160°．
故答案为：160°．
【题目】为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同．例如：若规定用量为10吨，每月用水量不超过10吨按1.5元/吨收费，超出10吨的部分按2元/吨收费，则某户居民一个月用水8吨，则应缴水费：8×1.5=12（元）；某户居民一个月用水13吨，则应缴水费：10×1.5+（13﹣10）×2=21（元）．
表是小明家1至4月份用水量和缴纳水费情况，根据表格提供的数据，回答：
月份 | 一 | 二 | 三 | 四 |
用水量（吨） | 6 | 7 | 12 | 15 |
水费（元） | 12 | 14 | 28 | 37 |
（1）该市规定用水量为 吨，规定用量内的收费标准是 元/吨，超过部分的收费标准是 元/吨．
（2）若小明家五月份用水20吨，则应缴水费 元．
（3）若小明家六月份应缴水费46元，则六月份他们家的用水量是多少吨？
