Question

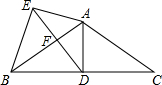如图，已知AB=AC，AD⊥BC于点D，AD=AE，AB平分∠DAE交DE于点F．
（1）请你写出图中三对全等三角形；
（2）求证：AE⊥BE．

Answer 1

分析：（1）本题考查的是全等三角形的判定的有关知识，可根据全等三角形的判定定理进行求解，答案不唯一．
（2）通过△AEB≌△ADB的对应角相等即可证得AE⊥BE．

解答：（1）解：△ADB≌△ADC、△ABD≌△ABE、△AFD≌△AFE、△BFD≌△BFE、△ABE≌△ACD（写出其中的三对即可）．

（2）证明：∵AD=AE，AB平分∠DAE交DE于点F．
∴∠EAB=∠DAB．
∴在△AEB与△ADB中，

AB=AB(公共边) ∠EAB=∠DAB AE=AD

，
∴△AEB≌△ADB（SAS），
∴∠AEB=∠ADB（全等三角形的对应角相等）．
∵AD⊥BC，
∴∠ADB=90°，
∴∠AEB=90°，即AE⊥BE．

点评：这是一道考查三角形全等的识别方法的开放性题目，答案可有多种，做题时从已知开始思考，结合判定方法由易到难逐个验证，做到不重不漏．