题目内容
在平面直角坐标系xOy中,点P是抛物线:y=x2上的动点(点在第一象限内).连接 OP,过点0作OP的垂线交抛物线于另一点Q.连接PQ,交y轴于点M.作PA丄x轴于点A,QB丄x轴于点B.设点P的横坐标为m.
(1)如图1,当m= 时,
时,
①求线段OP的长和tan∠POM的值;
②在y轴上找一点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标;
(2)如图2,连接AM、BM,分别与OP、OQ相交于点D、E.
①用含m的代数式表示点Q的坐标;
②求证:四边形ODME是矩形.

解:(1)①∵把x= 代入 y=x2,得 y=2,
代入 y=x2,得 y=2,
∴P( ,2),
,2),
∴OP=
∵PA丄x轴,
∴PA∥MO.
∴tan∠P0M=tan∠0PA=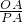 =
= .
.
②设 Q(n,n2),
∵tan∠QOB=tan∠POM,
∴ .
.
∴n=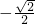
∴Q(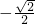 ,
, ),
),
∴OQ= .
.
当OQ=OC时,则C1(0, ),C2(0,
),C2(0,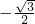 );
);
当OQ=CQ时,则C3(0,1);
当CQ=CO时,OQ为底,不合题意.
综上所述,当△OCQ是以OQ为腰的等腰三角形时,所求点C坐标为:C1(0, ),C2(0,
),C2(0,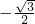 ),C3(0,1);
),C3(0,1);
(2)①设 Q(n,n2),
∵△APO∽△BOQ,
∴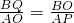
∴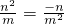 ,得n=
,得n= ,
,
∴Q( ,
,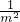 ).
).
②设直线PQ的解析式为:y=kx+b,把P(m,m2)、Q( ,
,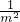 )代入,得:
)代入,得:
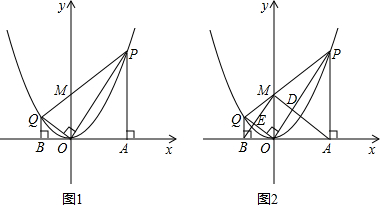
 ,
,
①-②得:m2-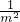 =(m+
=(m+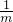 )k,
)k,
解得:k=m-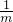 ③,
③,
把③代入①,得:b=1,
∴M(0,1)
∵ ,∠QBO=∠MOA=90°,
,∠QBO=∠MOA=90°,
∴△QBO∽△MOA
∴∠MAO=∠QOB,
∴QO∥MA
同理可证:EM∥OD
又∵∠EOD=90°,
∴四边形ODME是矩形.
分析:(1)①已知m的值,代入抛物线的解析式中可求出点P的坐标;由此确定PA、OA的长,通过解直角三角形易得出结论.
②题干要求△OCQ是以OQ为腰的等腰三角形,所以分QO=OC、QC=QO、CQ=CO三种情况来判断:
QO=QC时,Q在线段OC的垂直平分线上,Q、O的纵坐标已知,C点坐标即可确定;
QO=OC时,先求出OQ的长,那么C点坐标可确定;
CQ=CO时,OQ为底,不合题意.
(2)①由∠QOP=90°,易求得△QBO∽△MOA,通过相关的比例线段来表示出点Q的坐标;
②在四边形ODME中,已知了一个直角,只需判定该四边形是平行四边形即可,那么可通过证明两组对边平行来得证.
点评:考查了二次函数综合题,该题涉及的知识点较多,有:解直角三角形、相似三角形、等腰直角三角形的判定、矩形的判定等重要知识点;(1)②题中,要注意分类进行讨论,以免出现漏解、错解的情况.
 代入 y=x2,得 y=2,
代入 y=x2,得 y=2,∴P(
 ,2),
,2),∴OP=

∵PA丄x轴,
∴PA∥MO.
∴tan∠P0M=tan∠0PA=
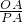 =
= .
.②设 Q(n,n2),
∵tan∠QOB=tan∠POM,
∴
 .
.∴n=
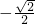
∴Q(
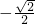 ,
, ),
),∴OQ=
 .
.当OQ=OC时,则C1(0,
 ),C2(0,
),C2(0,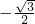 );
);当OQ=CQ时,则C3(0,1);
当CQ=CO时,OQ为底,不合题意.
综上所述,当△OCQ是以OQ为腰的等腰三角形时,所求点C坐标为:C1(0,
 ),C2(0,
),C2(0,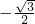 ),C3(0,1);
),C3(0,1);(2)①设 Q(n,n2),
∵△APO∽△BOQ,
∴
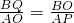
∴
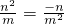 ,得n=
,得n= ,
,∴Q(
 ,
,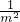 ).
).②设直线PQ的解析式为:y=kx+b,把P(m,m2)、Q(
 ,
,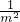 )代入,得:
)代入,得:
 ,
,①-②得:m2-
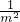 =(m+
=(m+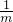 )k,
)k,解得:k=m-
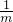 ③,
③,把③代入①,得:b=1,
∴M(0,1)
∵
 ,∠QBO=∠MOA=90°,
,∠QBO=∠MOA=90°,∴△QBO∽△MOA
∴∠MAO=∠QOB,
∴QO∥MA
同理可证:EM∥OD
又∵∠EOD=90°,
∴四边形ODME是矩形.
分析:(1)①已知m的值,代入抛物线的解析式中可求出点P的坐标;由此确定PA、OA的长,通过解直角三角形易得出结论.
②题干要求△OCQ是以OQ为腰的等腰三角形,所以分QO=OC、QC=QO、CQ=CO三种情况来判断:
QO=QC时,Q在线段OC的垂直平分线上,Q、O的纵坐标已知,C点坐标即可确定;
QO=OC时,先求出OQ的长,那么C点坐标可确定;
CQ=CO时,OQ为底,不合题意.
(2)①由∠QOP=90°,易求得△QBO∽△MOA,通过相关的比例线段来表示出点Q的坐标;
②在四边形ODME中,已知了一个直角,只需判定该四边形是平行四边形即可,那么可通过证明两组对边平行来得证.
点评:考查了二次函数综合题,该题涉及的知识点较多,有:解直角三角形、相似三角形、等腰直角三角形的判定、矩形的判定等重要知识点;(1)②题中,要注意分类进行讨论,以免出现漏解、错解的情况.

练习册系列答案
相关题目
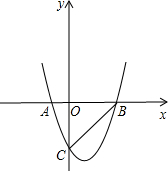 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为