题目内容
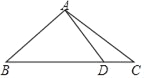
【题目】如图,已知点A、B、C、D均在已知圆上,AD∥BC, AC平分∠BCD, 请找出图中与弦AD相等的线段,并加以证明
【答案】解:∵AC平分∠BCD,
∴∠ACB=∠ACD,
∴ AD=AB
∵AD∥BC,
∴ ∠DAC=∠ACB
∴∠DAC=∠DCA
∴AD=CD,
∴AD=AB=CD.
【解析】由AC平分∠BCD得出∠ACB=∠ACD,证得AD=AB,再由AD∥BC及等量代换,证出∠DAC=∠DCA,得出AB=CD,即可得出结论。
【考点精析】利用角的平分线和平行线的性质对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目