题目内容
【题目】如图,将矩形![]() 沿
沿![]() 折叠后点
折叠后点![]() 与
与![]() 重合.若原矩形的长宽之比为
重合.若原矩形的长宽之比为![]() ,则
,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据折叠的性质得到ED′=BE,∠D′EF=∠BEF,根据平行线的性质得到∠D′EF=∠EFB,求得BE=BF,设AD′=BC′=3x,AB=x,根据勾股定理得到BE=![]() x,于是得到结论.
x,于是得到结论.
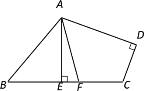
如图,将矩形ABCD沿EF折叠后点D与B重合,
∴ED′=BE,∠D′EF=∠BEF,
∵AD′∥BC′,
∴∠D′EF=∠EFB,
∴∠BEF=∠EFB,
∴BE=BF,
∵原矩形的长宽之比为3:1,
∴设AD′=BC′=3x,AB=x,
∴AE=3xED′=3xBE,
∵AE2+AB2=BE2,
∴(3xBE)2+x2=BE2,
解得:BE=![]() x,
x,
∴BF=BE=![]() x,AE=3xBE=
x,AE=3xBE=![]() x
x
∴![]() =
=![]() =
=![]() ,
,
故选:D.


练习册系列答案
相关题目