Question

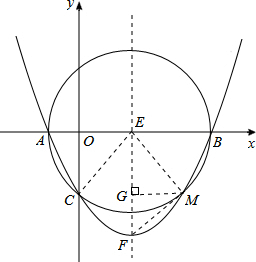
如图，已知以E（3，0）为圆心，以5为半径的⊙E与x轴交于A，B两点，与y轴交于C点，抛物线y=ax²+bx+c经过A，B，C三点，顶点为F．
（1）求A，B，C三点的坐标；
（2）求抛物线的解析式及顶点F的坐标；
（3）已知M为抛物线上一动点（不与C点重合），试探究：
①使得以A，B，M为顶点的三角形面积与△ABC的面积相等，求所有符合条件的点M的坐标；
②若探究①中的M点位于第四象限，连接M点与抛物线顶点F，试判断直线MF与⊙E的位置关系，并说明理由．

Answer 1

（1）∵以E（3，0）为圆心，以5为半径的⊙E与x轴交于A，B两点，
∴A（-2，0），B（8，0）．
如解答图所示，连接CE．
在Rt△OCE中，OE=AE-OA=5-2=3，CE=5，
由勾股定理得：OC=

CE2-OE2

=

52-32

=4．
∴C（0，-4）．

（2）∵点A（-2，0），B（8，0）在抛物线上，
∴可设抛物线的解析式为：y=a（x+2）（x-8）．
∵点C（0，-4）在抛物线上，
∴-4=a×2×-8，解得a=

1

4

．
∴抛物线的解析式为：y=

1

4

（x+2）（x-8）=

1

4

x²-

3

2

x-4=

1

4

（x-3）²-

25

4

∴顶点F的坐标为（3，-

25

4

）．

（3）①∵△ABC中，底边AB上的高OC=4，
∴若△ABC与△ABM面积相等，则抛物线上的点M须满足条件：|y_M|=4．
（I）若y_M=4，则

1

4

x²-

3

2

x-4=4，
整理得：x²-6x-32=0，解得x=3+

41

或x=3-

41

．
∴点M的坐标为（3+

41

，4）或（3-

41

，4）；
（II）若y_M=-4，则

1

4

x²-

3

2

x-4=-4，
整理得：x²-6x=0，解得x=6或x=0（与点C重合，故舍去）．
∴点M的坐标为（6，-4）．
综上所述，满足条件的点M的坐标为：（3+

41

，4），（3-

41

，4）或（6，-4）．
②直线MF与⊙E相切．理由如下：
由题意可知，M（6，-4）．
如解答图所示，连接EM，MF，过点M作MG⊥对称轴EF于点G，
则MG=3，EG=4．
在Rt△MEG中，由勾股定理得：ME=

MG2+EG2

=

32+42

=5，
∴点M在⊙E上．
由（2）知，顶点F的坐标（3，-

25

4

），∴EF=

25

4

，
∴FG=EF-EG=

9

4

．
在Rt△MGF中，由勾股定理得：MF=

MG2+FG2

=

32+( 9 4 )2

=

15

4

．
在△EFM中，∵EM²+MF²=5²+（

15

4

）²=（

25

4

）²=EF²，
∴△EFM为直角三角形，∠EMF=90°．
∵点M在⊙E上，且∠EMF=90°，
∴直线MF与⊙E相切．