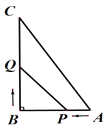题目内容
【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E,F是BC上一点,且CF=AE,连接DF.

(1)求证DF∥BE;
(2)若∠ABC=70°,求∠CDF的度数.
【答案】(1)证明见解析;(2)∠CDF=35°.
【解析】
(1)根据平行四边形ABCD的性质证明四边形BEDF是平行四边形,最后根据平行四边形对边平行得出结论;
(2)由平行四边形的性质得出∠ABC=∠ADC,∠EBF=∠EDF,最后根据∠CDF=∠ADC﹣∠EDF进行求解.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵CF=AE,
∴DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形,
∴DF∥BE;
(2)解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=70°,
∵BE平分∠ABC,
∴∠EBF=![]() ∠ABC=35°,
∠ABC=35°,
∵四边形BEDF是平行四边形,
∴∠EBF=∠EDF=35°,
∴∠CDF=∠ADC﹣∠EDF=35°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】养牛场的李大叔分三次购进若干头大牛和小牛.其中有一次购买大牛和小牛的价格同时打折,其余两次均按原价购买,三次购买的数量和总价如下表:
(1)李大叔以折扣价购买大牛和小牛是第 次;是打 折.
(2)用解方程(组)的方法求大牛和小牛的原价.
大牛(头) | 小牛(头) | 总价(元) | |
第一次 | 4 | 3 | 9900 |
第二次 | 2 | 6 | 9000 |
第三次 | 6 | 9 | 13230 |